Question

Choose the correct option provided below for the following question.
A man standing on a horizontal plane, observes the angle of elevation of the top of a tower to be $\alpha$. After walking a distance equal to double the height of the tower, the angle of the elevation becomes $2\alpha$, then $\alpha$ is equal to
A. $\dfrac{\pi }{2}$
B. $\dfrac{\pi }{6}$
C. $\dfrac{\pi }{{12}}$
D. $\dfrac{\pi }{{18}}$

Answer 1

We draw a diagram, representing all the given conditions. We assume the height of the tower to be a variable and divide the diagram into two terms. Since the triangles are right-angled, we can use trigonometry to find the relation between the two given angles. Once we get the angle using the substitution and trigonometric ratios, we get the solution.

Complete step-by-step solution:
First, draw a diagram representing the given elements to make the solution solving easy.

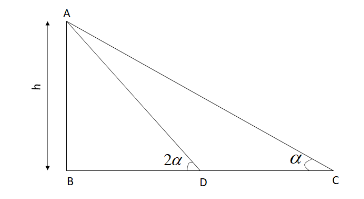
Given, the angle of elevation from a point to the tower $= \alpha$
The angle of elevation from the point after walking twice the distance $= 2\alpha$
Let us assume that the height of the tower is $h$
Since the distance walked to a point where the angle of elevation is $2\alpha$, that is $CD$ is twice the height, we get:
$CD = 2h$
Taking $\vartriangle ABC$,
$\tan \alpha = \dfrac{h}{{BC}}$
Writing $BC$ in simple terms, that is $BC = BD + DC$
$\Rightarrow \tan \alpha = \dfrac{h}{{BD + 2h}}$
In $\vartriangle ABD$,
$\tan 2\alpha = \dfrac{h}{{BD}}$
Expanding the formula of $\tan 2\alpha$, we get:
$\Rightarrow \dfrac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }} = \dfrac{h}{{BD}}$
Substituting the value of $\tan \alpha$ evolved before in the above equation, we get:
$\Rightarrow \dfrac{{2\left( {\dfrac{h}{{BD + 2h}}} \right)}}{{1 - {{\left( {\dfrac{h}{{BD + 2h}}} \right)}^2}}} = \dfrac{h}{{BD}}$
Simplifying the above equation, we get;
$\Rightarrow \dfrac{{\dfrac{{2h}}{{BD + 2h}}}}{{\dfrac{{{{\left( {BD + 2h} \right)}^2} - {h^2}}}{{{{\left( {BD + 2h} \right)}^2}}}}} = \dfrac{h}{{BD}}$
Rearranging the terms and taking the reciprocals and cancelling the common terms of the denominator, we get:
$\Rightarrow \dfrac{{2h\left( {BD + 2h} \right)}}{{{{\left( {BD + 2h} \right)}^2} - {h^2}}} = \dfrac{h}{{BD}}$
Cancelling out the $h$ from the numerator on the both sides and expanding the denominator;
$\Rightarrow \dfrac{{2\left( {BD + 2h} \right)}}{{B{D^2} + 4{h^2} + 4hBD - {h^2}}} = \dfrac{1}{{BD}}$
Cross multiplying the given terms, we get:
$\Rightarrow 2B{D^2} + 4hBD = B{D^2} + 3{h^2} + 4hBD$
Rearranging the terms and subtracting the common terms;
$\Rightarrow B{D^2} = 3{h^2}$
Taking square-root on both the sides,
$\Rightarrow BD = \sqrt {3{h^2}}$
$\Rightarrow BD = \sqrt 3 h$
Now, getting the value of $BD$, we substitute the value obtained in $\tan \alpha$.
$\tan \alpha = \dfrac{h}{{\sqrt 3 h + 2h}}$
Taking $h$ common from the denominator;
\Rightarrow$$$\tan \alpha = \dfrac{h}{{\left( {\sqrt 3 + 2} \right)h}}$$ Cancelling the common terms; \Rightarrow\tan \alpha = \dfrac{1}{{\left( {\sqrt 3 + 2} \right)}}$$ Taking the inverse, $\Rightarrow\alpha = {\tan ^{ - 1}}\dfrac{1}{{\left( {\sqrt 3 + 2} \right)}} Rationalizing the terms of the denominator; $\Rightarrow$$$\alpha = {\tan ^{ - 1}}\dfrac{{\left( {\sqrt 3 - 2} \right)}}{{\left( {\sqrt 3 + 2} \right)\left( {\sqrt 3 - 2} \right)}}
Using $\left( {a + b} \right)\left( {a - b} \right) = \left( {{a^2} - {b^2}} \right)$ we get,
\Rightarrow$$$\alpha = {\tan ^{ - 1}}\dfrac{{\left( {\sqrt 3 - 2} \right)}}{{\left( {3 - 4} \right)}}$$ Subtracting we get, \Rightarrow\alpha = {\tan ^{ - 1}}\dfrac{{\left( {\sqrt 3 - 2} \right)}}{{ - 1}}$$ Taking the negative symbol to the numerator, we get the additive inverse; $\Rightarrow\alpha = {\tan ^{ - 1}}\left( {2 - \sqrt 3 } \right)$Since the value of$2 - \sqrt 3 = \tan \dfrac{\pi }{{12}} $\Rightarrow$$$\alpha = {\tan ^{ - 1}}\tan \dfrac{\pi }{{12}}
The inverse is cancelled with the value:
$\Rightarrow \alpha = \dfrac{\pi }{{12}}$
Now we get the value of $\alpha = \dfrac{\pi }{{12}}$.

$\therefore$ The correct option is C.

Note: We have to remember that, angles of elevation and depression are angles that are formed with the horizontal plane. If the line of sight is upward from the horizontal, the angle is an angle of elevation, if the line of sight is downward from the horizontal, the angle is an angle of depression. These types of angles and some trigonometry can be used to indirectly calculate heights of objects or distances between points. Alternatively, if the heights or distances are known, the angles can be determined. Elevation is the height of a geographic location above a fixed reference point.