Question
Question: Choose the correct answer from among the given ones: The gravitational intensity at the centre of ...
Choose the correct answer from among the given ones:
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow in the above figure.
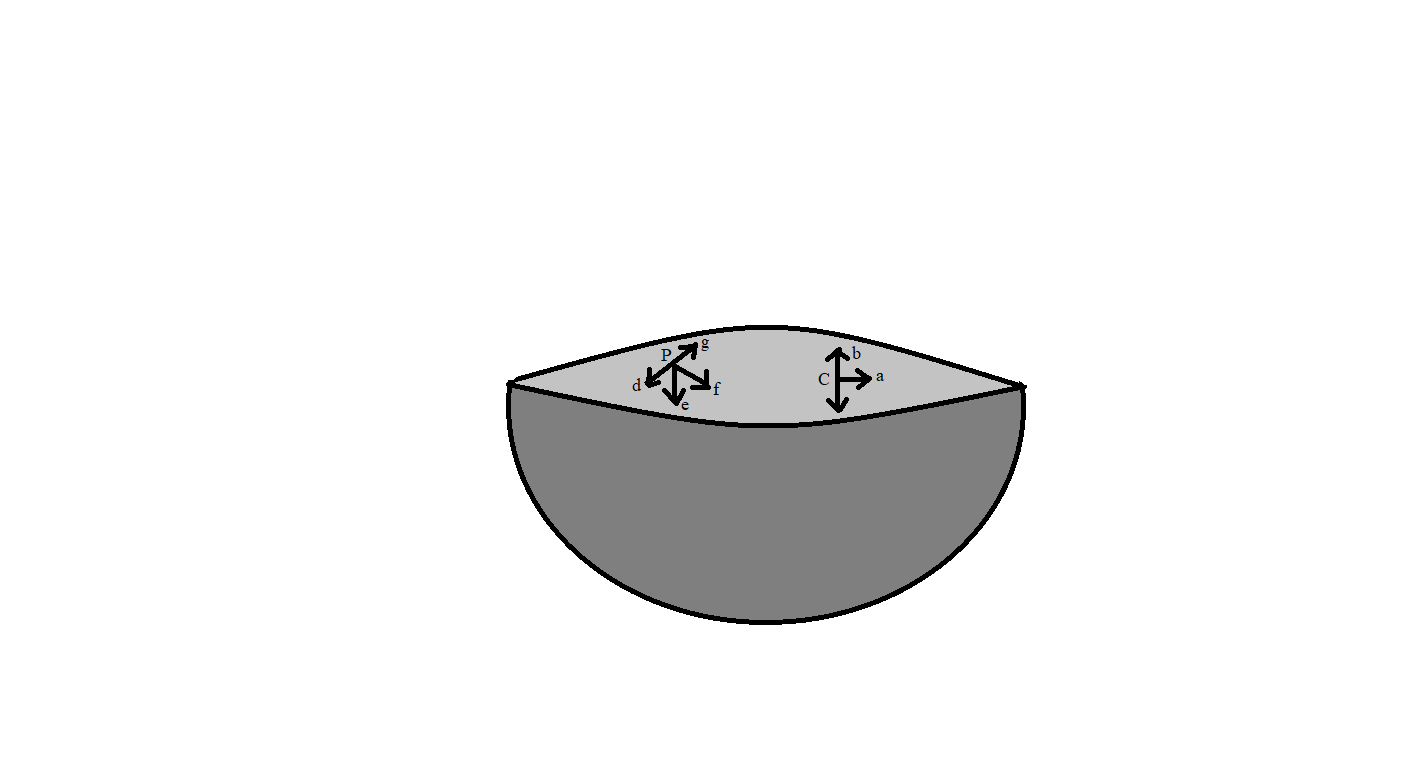
A. a
A. b
C. c
D. d
Solution
Hint: Assume hemispherical shell as it is a part of spherical shell being cut into half. To find the direction of the gravitational intensity, we need to apply the fact that in the case of spherical shells, gravitational potential is constant throughout. So when the sphere will cut into two equal halves, what effect will fall on the gravitational intensity.
Complete step by step answer:
Gravitational field is described as the region of space surrounding a body in which another body experiences a force of gravitational attraction.
Gravitational intensity is defined as the measurement of the force that is experienced by a unit mass in the given field. Its unit is Nkg−1.
Gravitational potential at a position is equal to the amount of work per unit mass that would be needed to move a body to that position. Its unit is Joule kg−1.
Potential energy is a property of a system rather than of a single object, due to its physical position. An object’s potential is due to its position relative to the surroundings within the Earth-object system.
We know that the gravitational potential in a sphere is constant throughout. Also, the gravitational intensity will act in the downward direction as its upper half is cut, gravitational force will also act in downward direction. Thus, the required direction of gravitational intensity is shown by the arrow.
We know that the gravitational potential V in a sphere is constant throughout. Also, the gravitational intensity will act in the downward direction as its upper half is cut, gravitational force will also act in downward direction. Thus, the required direction of gravitational intensity is shown by the arrow c.
Hence, the correct option is C.
Note: Due to zero gravitational force on any particle at any point inside a spherical shell, if we remove the upper half of the sphere, the net gravitational force at any particle in the shell will act downward.
