Solveeit Logo
Login

Question

Question: Charges \(+q\) and \(-q\) are placed at points A and B respectively which are a distance \(2L\) apar...

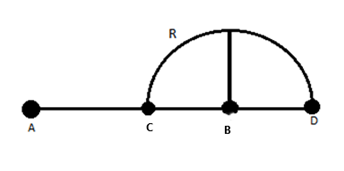
Charges +q+q and −q-q are placed at points A and B respectively which are a distance 2L2L apart, C is the midpoint between A and B. The work done in moving a charge +Q+Qalong the semicircle CRD is
A. qQ2πε0L\dfrac{qQ}{2\pi {{\varepsilon }_{0}}L}
B. qQ6πε0L\dfrac{qQ}{6\pi {{\varepsilon }_{0}}L}
C. −qQ6πε0L-\dfrac{qQ}{6\pi {{\varepsilon }_{0}}L}
D. qQ4πε0L\dfrac{qQ}{4\pi {{\varepsilon }_{0}}L}

Explanation

Solution

The work done by an electric force is proportional to the amount of the moved charge and proportional to the difference of potentials between the starting point and the destination.
W(r)=Q×V(r){{W}_{(r)}}=Q\times {{V}_{(r)}}
Potential at a distance ‘r’ from the center of a dipole is given by:
V(r)=k2aqcos⁡θr2−a2cos⁡2θ{{V}_{\left( r \right)}}=\dfrac{k2aq\cos \theta }{{{r}^{2}}-{{a}^{2}}{{\cos }^{2}}\theta }
Where;
2a is distance between the two charges of the dipole
q is the magnitude of charge of the dipole
k=14πεok=\dfrac{1}{4\pi {{\varepsilon }_{o}}}

Complete answer:
It is given in the question that ′2L′'2L'is the distance between the two charges of the dipole with point C as the center of the dipole.
Since the external charge ′+Q′'+Q' undergoes a semicircular path from C to a point D with the center of the trajectory at point B. Hence, the radius of this semicircular path will be ′L′'L'.
Potential at the center of the dipole is 00 .
This is because, at C:
VC=V+q+V−q{{V}_{C}}={{V}_{+q}}+{{V}_{-q}}
VC=kqL+k(−q)L{{V}_{C}}=\dfrac{kq}{L}+\dfrac{k(-q)}{L}
Therefore,
VC=0{{V}_{C}}=0
Potential at point D due to the dipole is:
VD=k(2Lq)cos⁡θ(2L)2−(Lcos⁡θ)2{{V}_{D}}=\dfrac{k(2Lq)\cos \theta }{{{(2L)}^{2}}-{{(L\cos \theta )}^{2}}}
Since D lies on an axial position with respect to the dipole, θ=180o\theta ={{180}^{o}}
Therefore cos⁡θ=−1\cos \theta =-1
⇒\Rightarrow VD=−k(2Lq)3(L)2{{V}_{D}}=-\dfrac{k(2Lq)}{3{{(L)}^{2}}}
∵\because k=14πεok=\dfrac{1}{4\pi {{\varepsilon }_{o}}}
VD=−(2q)4πεo(3L){{V}_{D}}=-\dfrac{(2q)}{4\pi {{\varepsilon }_{o}}(3L)}
VD=−(q)6πεo(L){{V}_{D}}=-\dfrac{(q)}{6\pi {{\varepsilon }_{o}}(L)}
The work done to move ′+Q′'+Q' from point C to D is:
WCD=Q[VD−Vc]{{W}_{CD}}=Q[{{V}_{D}}-{{V}_{c}}]
WCD=Q[−(q)6πεo(L)−0]{{W}_{CD}}=Q[-\dfrac{(q)}{6\pi {{\varepsilon }_{o}}(L)}-0]
WCD=−Q(q)6πεo(L){{W}_{CD}}=-\dfrac{Q(q)}{6\pi {{\varepsilon }_{o}}(L)}
Hence the correct option will be option C) −Q(q)6πεo(L)-\dfrac{Q(q)}{6\pi {{\varepsilon }_{o}}(L)}

Note:
The work done to move charge ′+Q′'+Q' from point C to point D is independent of the path undertaken and depends only on the initial and final positions of the charge.
Since the point D is closer to −q-q, the net potential at point D will be negative in magnitude.