Question

Charges $Q$ , $2Q$ and $4Q$ are uniformly distributed in three dielectric solid spheres 1, 2 and 3 of radii $\dfrac{R}{2}$ , $R$ and $2R$ respectively, as shown in the figure. If magnitudes of the electric fields at point P and at a distance $R$ from the center of the sphere 1, 2 and 3 are ${E_1}$ , ${E_2}$ and ${E_3}$ respectively, then:

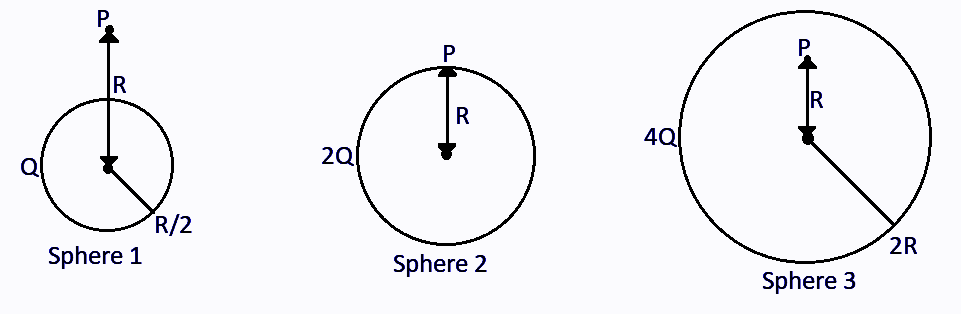
(A) ${E_1} > {E_2} > {E_3}$
(B) ${E_3} > {E_1} > {E_2}$
(C) ${E_2} > {E_1} > {E_3}$
(D) ${E_3} > {E_2} > {E_1}$

Answer 1

Hint
We need to solve this problem using Gauss's law for electrostatics. Using the gauss’s law we need to calculate the electric field at the point P due to all the three cases. Then comparing the values we will get the answer.

Formula Used: In this solution we will be using the following formula,
$\Rightarrow \int {E \cdot dS} = \dfrac{Q}{{{\varepsilon _o}}}$
Where $E$ is the electric field, is the surface area, $Q$ is the charge enclosed by the surface $S$ and ${\varepsilon _o}$ is the permittivity in free space.

Complete step by step answer
To solve this problem, we need to apply the Gauss’s law of electrostatics in all the three cases to find the electric field. Let us consider sphere 1.
Here, the Gaussian surface as,

The dotted line represents the gaussian surface of radius $R$
Now applying the Gauss’s law we get,
$\Rightarrow \int {{E_1} \cdot dS} = \dfrac{{{Q_1}}}{{{\varepsilon _o}}}$
Here the electric field will be constant and come out of the integration. The total surface will be the surface area of the dotted sphere, and the total charge will be all the charge contained within the dotted circle. Therefore we have,
$\Rightarrow {E_1} \times 4\pi {R^2} = \dfrac{Q}{{{\varepsilon _o}}}$
Hence we get ${E_1}$ as,
$\Rightarrow {E_1} = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{Q}{{{R^2}}}$
Now for sphere 2, the Gaussian surface will be the same as the surface of the sphere.

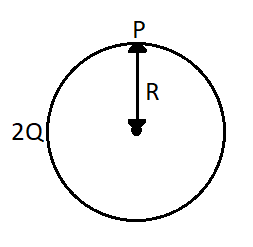
Therefore from the Gauss’s law again we get,
$\Rightarrow \int {{E_2} \cdot dS} = \dfrac{{{Q_2}}}{{{\varepsilon _o}}}$
Here the electric field will be constant and come out of the integration. The total surface will be the surface area of the sphere, and the total charge will be all the charge contained within the sphere. Therefore we have,
$\Rightarrow {E_2} \times 4\pi {R^2} = \dfrac{{2Q}}{{{\varepsilon _o}}}$
Hence we get ${E_2}$ as,
$\Rightarrow {E_2} = 2 \times \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{Q}{{{R^2}}}$
Which is equal to ${E_2} = 2{E_1}$
Now for sphere 3, the Gaussian surface will be again given by the dotted sphere as in the diagram.
Therefore from the Gauss’s law again we get,
$\Rightarrow \int {{E_3} \cdot dS} = \dfrac{{{Q_3}}}{{{\varepsilon _o}}}$
Here the electric field will be constant and come out of the integration. The total surface will be the surface area of the dotted sphere.

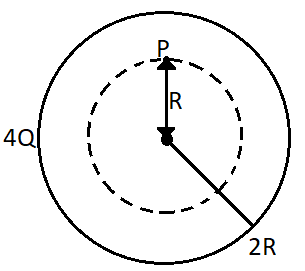
The total charge in this sphere will be given by the charge that is contained in the dotted sphere.
Therefore, ${Q_3} = \dfrac{{4Q}}{{\dfrac{4}{3}\pi {{\left( {2R} \right)}^3}}} \times \dfrac{4}{3}\pi {R^3}$
So on cancelling the like terms, we get
$\Rightarrow {Q_3} = \dfrac{{4Q}}{8}$
Therefore we get the charge enclosed as,
$\Rightarrow {Q_3} = \dfrac{Q}{2}$
Therefore on substituting we have,
$\Rightarrow {E_3} \times 4\pi {R^2} = \dfrac{Q}{{2{\varepsilon _o}}}$
Hence we get ${E_3}$ as,
$\Rightarrow {E_3} = \dfrac{1}{2} \times \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{Q}{{{R^2}}}$
Which is equal to ${E_3} = \dfrac{1}{2}{E_1}$
Therefore, we get from the three values of electric field,
$\Rightarrow {E_2} > {E_1} > {E_3}$
So the correct option is C.

Note
Gauss's law in electrostatics relates the distribution of the electric charge to the electric field. It states that the flux of electric field out of an arbitrary closed surface is proportional to the electric charge enclosed by the surface.