Question

Charges of $5\mu C$ each are placed at the corners of an equilateral triangle of side 10 cm. Then the force on each charge is:-
(A) 78 N
(B) 39 N
(C) 29 N
(D) 22.5 N

Answer 1

Hint : Since this is an equilateral triangle the angles as well as the length of the sides will be equal. The net resultant force acting on all the vertices of A, B, C of the equilateral triangle will be the sum of the forces due to the charge on the other two vertices.

Formula used: The formulae used in the solution are given here.
$F = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$ where $F$ is the electrical force between two charged objects, ${q_1}$ represents the quantity of charge on object 1 (in Coulombs), ${q_2}$ represents the quantity of charge on object 2 (in Coulombs) and $r$ is the distance of separation between the two charges.

Complete step by step answer:
Given in the question, ABC is an equilateral triangle of side 10cm, where charges of $5\mu C$ are placed at the vertices A, B and C.

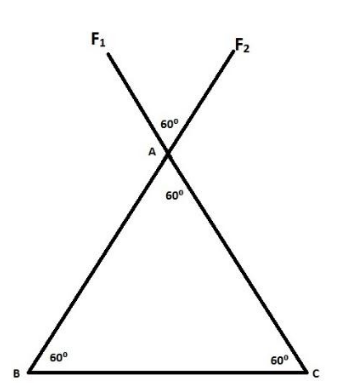
Three charges of equal magnitude are placed at the vertices of an equilateral triangle with side length 10cm. Let the force due to charge on vertex B be ${F_1}$ and due to the charge on vertex C be ${F_2}$ . It is quite evident that, since charges of $5\mu C$ are placed at the vertices of the equilateral triangle, which means the distance of separation is also the same-thus, the forces ${F_1}$ and ${F_2}$ are equal.
Using, $F = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$ where $F$ is the electrical force between two charged objects, ${q_1}$ represents the quantity of charge on object 1 (in Coulombs), ${q_2}$ represents the quantity of charge on object 2 (in Coulombs), $r$ is the distance of separation between the two charges and ${ \in _0}$ is the vacuum permittivity, permittivity of free space.
We get, ${F_1} = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{5^2} \times {{\left( {{{10}^{ - 6}}} \right)}^2}}}{{{{\left( {10 \times {{10}^{ - 2}}} \right)}^2}}}N$ where ${q_1} = {q_2} = 5 \times {10^{ - 6}}C$ and $r = 10 \times {10^{ - 2}}m$ .
and, ${F_1} = {F_2}$ . Thus, ${F_1} = {F_2} = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{5^2} \times {{\left( {{{10}^{ - 6}}} \right)}^2}}}{{{{\left( {10 \times {{10}^{ - 2}}} \right)}^2}}}N$ .
Assigning the value of $\dfrac{1}{{4\pi { \in _0}}} = 9 \times {10^9}$ ,
${F_1} = 9 \times {10^9} \times \dfrac{{{5^2} \times {{\left( {{{10}^{ - 6}}} \right)}^2}}}{{{{\left( {10 \times {{10}^{ - 2}}} \right)}^2}}}N$
$\Rightarrow {F_1} = 2.25 \times 10 = 22.5N$
The angles between the sides of an equilateral triangle is ${60^ \circ }$ . So the resultant of the two forces is given by ${F_{net}}$ where, ${F_{net}} = \sqrt {{F_1}^2 + {F_2}^2 + 2{F_1}{F_2}\cos {{60}^ \circ }}$ .
Since ${F_1} = {F_2}$ so we can write,
${F_{net}} = \sqrt {{F_1}^2 + {F_1}^2 + 2{F_1}{F_1}\cos {{60}^ \circ }}$
$\Rightarrow {F_{net}} = \sqrt {2{F_1}^2 + 2{F_1}^2 \times \dfrac{1}{2}}$
On calculating we get the net force as,
${F_{net}} = \sqrt 3 {F_1}$
Now substituting the value of ${F_1}$ we get,
${F_{net}} = \sqrt 3 \times 22.5 = 38.97N \simeq 39N$
Hence the correct answer is option D, 39N.

Note:
The resultant of the two forces is given by ${F_{net}}$ where, ${F_{net}}$ will be the vector sum of the forces ${F_1}$ and ${F_2}$ acting on the charge as shown in the figure. Since the angle between the sides of an equilateral triangle is ${60^ \circ }$ , so the angle between the forces will also be ${60^ \circ }$ .