Question

Charges are placed on the vertices of a square as shown. Let $\vec E$ be the electric field and V be the potential at the centre. If the charges on A and B are interchanged with those on D and C respectively, then:

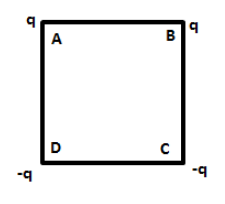
A. $\vec E$ remains unchanged, V changes
B. Both $\vec E$ and V change
C. $\vec E$ and V remain unchanged
D. $\vec E$ changes, V remains unchanged

Answer 1

The electric field is a vector quantity that means it has direction but the potential is a scalar quantity. The potential at a point is the sum of potentials due to each charge. Calculate the direction of the net electric field at the centre before and after the charges are interchanged. If the direction of the net electric field is different, the electric field is considered to be changed.

Formula used:
Potential, $V = k\dfrac{q}{d}$, where, k is the constant, q is the charge and d is the distance.
Electric field, $E = k\dfrac{q}{{{d^2}}}$

Complete step by step answer:
We know that the electric field is a vector quantity that means it has direction but the potential is a scalar quantity. We assume the distance of every vertex from the centre of the square is d.

We know that for the system of charges, the potential at a point is the sum of potentials due to each charge. Let’s express the potential at the centre of the square before the charges are interchanged as follows,
$V = {V_A} + {V_B} + {V_C} + {V_D}$
$\Rightarrow V = k\dfrac{q}{d} + k\dfrac{q}{d} + k\dfrac{{ - q}}{d} + k\dfrac{{ - q}}{d}$
$\Rightarrow V = 0$

Even after we interchange the charges, the potential at the centre will remain the same that is zero. Now, let’s express the direction of electric field due to each charge before the charges are interchanged as follows,

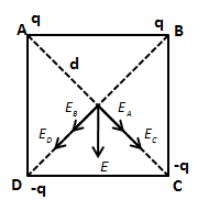
Therefore, the net electric field is in the downward direction. Now, the charges on A and B are interchanged with charges on C and D, the direction of the field will be as shown in the figure below.

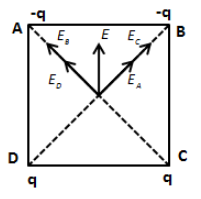
Thus, we can see that the direction of the net electric field is changed after interchanging the charges. However, the magnitude of the electric field will remain the same. But since the electric field is the vector quantity, the electric field changes after interchanging the charges.

So, the correct answer is option D.

Note: Students can express the net electric field as, $\vec E = {\vec E_x} + {\vec E_y}$. Here, ${\vec E_x}$ is the horizontal component of the net electric field and ${\vec E_y}$ is the vertical component of the net electric field. The magnitude of the electric field will change only when there is the change in the distance from the vertex. But since the distance remained the same, the magnitude of the electric field also remained the same.