Question

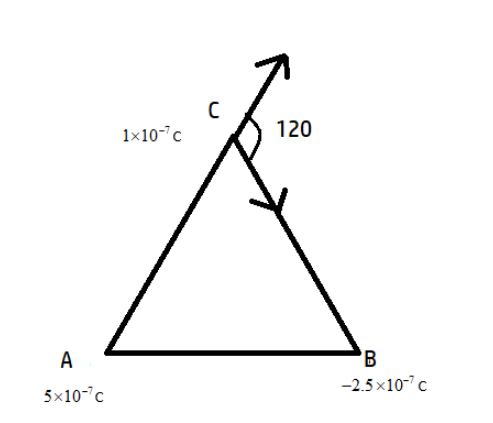
Charges $5\times {{10}^{-7}}$C, $-2.5\times {{10}^{-7}}$C and $1\times {{10}^{-7}}$C are held fixed at the three corners A, B and C of an equilateral triangle of side 10cm respectively. Find the electric force on the charge at C due to the rest two.

Answer 1

We are given with three charges placed at the corner of an equilateral triangle. Charges at A and C are positive and at B it is negative. In order to find out the force, we fix the charges at A and B and allow charge C to move. The direction of force acting charge C is shown. We can use coulomb’s law to solve this problem.

Complete step by step answer:
Side of triangle=AB=BC=CA= 10 cm= 0.1m

From Coulomb’s law force between two charges separated by a distance is given as $F=\dfrac{k{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$
Here k is a constant whose value is $9\times {{10}^{9}}N{{m}^{2}}/{{C}^{2}}$ and r=0.1 m
We have shown the direction of force between charges at A&C; and B&C;
For charges at A and C:
${{F}_{1}}=\dfrac{9\times {{10}^{9}}\times 5\times {{10}^{-7}}\times 1\times {{10}^{-7}}}{{{0.1}^{2}}}=0.045N$
For charges at B and C:
${{F}_{2}}=\dfrac{9\times {{10}^{9}}\times 2.5\times {{10}^{-7}}\times 1\times {{10}^{-7}}}{{{0.1}^{2}}}=0.0225N$
We have taken the magnitudes and direction is shown in the figure. Since force is a vector quantity adding the two forces using parallelogram law of vector addition.
$F=\sqrt{F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\cos \alpha }$, here $\alpha$is the angle between the two forces which is $120{}^\circ$
Putting the value, we get, $F=\sqrt{{{0.045}^{2}}+{{0.0225}^{2}}+2\times 0.045\times 0.0225\times \cos 120}$
$F=0.038N$

So, the magnitude of net force on charge C is 0.038N.

Note: Here we have found only magnitude because the question demand was only to find the net force. Had we also needed to find the direction then we will have to use trigonometry to further show the resultant force making angle with either of the forces.