Question

Charge $Q$, is divided into two parts which are then kept some distance apart. The force between them will be maximum if the two parts are having the charge
A) $\dfrac{Q}{2}$ each
B) $\dfrac{Q}{4}$ and $\dfrac{3Q}{4}$
C) $\dfrac{Q}{3}$ and $\dfrac{2Q}{3}$
D) $e$ and $(Q-e)$, where $e=$electronic charge

Answer 1

The force of attraction between two charged particles at a distance is given by Coulomb’s law. The force of attraction between two stationary, electrically charged particles is maximum when the first derivative of the maximum force with respect to one of the charges is equal to zero.

Complete answer:
Coulomb’s law states that the force of attraction between two stationary, electrically charged particles is equal to
$F=k\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$
where
$F$ is the force of attraction
${{q}_{1}}$ and ${{q}_{2}}$ are the stationary charges
$r$ is the distance between the charges
$k$ is the Coulomb’s constant
Let this be equation 1.
From the question, we are provided that a charge $Q$ is divided into two and the force of attraction between the divided charges is maximum. We are required to find these charges.
Let us assume one of these charges to be $q$. The other charge turns out to be $Q-q$. Also, let the distance between these two charges be $d$ as shown in the following figure.

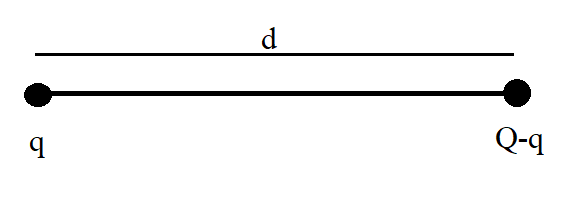
Applying equation 1 to these parameters, we have
$F=k\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}=k\dfrac{q(Q-q)}{{{d}^{2}}}$
Let this be equation 2.
Now, we are given that the force of attraction between the charges $Q$ and $Q-q$ is maximum.
For maximum force of attraction,
$\dfrac{d{{F}_{\max }}}{dq}=0$
Let this be equation 3.
Applying equation 2 in equation 3, we have
$\dfrac{d{{F}_{\max }}}{dq}=\dfrac{dk\dfrac{q(Q-q)}{{{d}^{2}}}}{dq}=0\Rightarrow \dfrac{k}{{{d}^{2}}}\dfrac{d\left[ q(Q-q) \right]}{dq}=0\Rightarrow \dfrac{d\left[ q(Q-q) \right]}{dq}=0$
On further simplification, we have
$\dfrac{d\left[ q(Q-q) \right]}{dq}=0\Rightarrow \dfrac{d(qQ-{{q}^{2}})}{dq}=0\Rightarrow Q-2q=0\Rightarrow q=\dfrac{Q}{2}$
Therefore, one of the charges is equal to $\dfrac{Q}{2}$. The other charge also turns out to be
$Q-q=Q-\dfrac{Q}{2}=\dfrac{Q}{2}$.

So, the correct answer is “Option A”.

Note:
The force determined through Coulomb’s law follows sign convention. If the stationary charges have opposite signs, then the force turns out to be negative and the nature of the force is attractive. If the stationary charges have the same signs, then the force turns out to be positive and the nature of the force is repulsive. Here, in this question, we have only dealt with the magnitude of force.