Question
Question: Charge \( - q\) and \( + q\) located at A and B, respectively, constitute an electric dipole. Distan...
Charge −q and +q located at A and B, respectively, constitute an electric dipole. Distance AB = 2a, O is the mid point of the dipole and OP is perpendicular to AB. A charge Q is placed at P where OP = y and y>>2a. The charge Q experiences and electrostatic force F. If Q is now moved along the equatorial line to P′ such that OP′=(3y) the force on Q will be close to L : (3y>>2a)
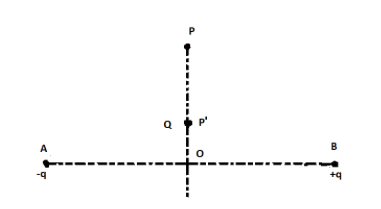
A) 3F
B) 3F
C) 9F
D) 27F
Solution
In order to solve this question one should be aware of the concept of electrostatic forces and how the net electrostatic force is calculated. Here, in this question, charge Q experiences force which is the resultant of both −q and +q. Also, remember that y>>2a. So, we can neglect a when higher powers are taken.
Complete step by step answer:
Here the charge Q will experience an electrostatic force due to both −q and +q, the force F is the resultant force applied by both −q and +q .
The electrostatic force between any two charges is given by
F=r2q1q2
Here q1 and q2 are the two charges.
r is the distance between the two charges.
Let the force applied by charge −q on Q when it is placed at point P be FA so FA would be given by
FA=(y2+a2)2qQ
As, y>>2a
So, FA=y2qQ
Similarly, Let the force applied by charge +q on Q when it is placed at point P be FB so FB would be given by FB=y2qQ
For the net force we have to calculate the resultant force on Q
Here, the components of sinθ would get cancelled and only cosθ component would be added.
So, F=FAcosθ+FBcosθ
Here, cosθ=y2+a2a
As, y>>2a
cosθ=ya
So, the net force would become, F=(FA+FB)×ya
F=(y22qQ)×ya
On simplifying we get,
F=y32aqQ ………. Equation 1
Now when the charge Q is put at P′
We have the distance between the charges as 3y
So, putting y as 3y in the equation 1 we get,
F′=27×(y32aqQ)
Hence, F′=27F
So, option D is the correct answer.
Note: Always remember that like charges repel each other and unlike or opposite charges attract each other. If two charges are at rest then the force between them is known as electrostatic force. This force between charges increases when the magnitude of the charges increases and also when the distance between the charges decreases.
