Question
Question: The minimum value of $2 \sin^2 \theta + 3 \cos^2 \theta$ is...
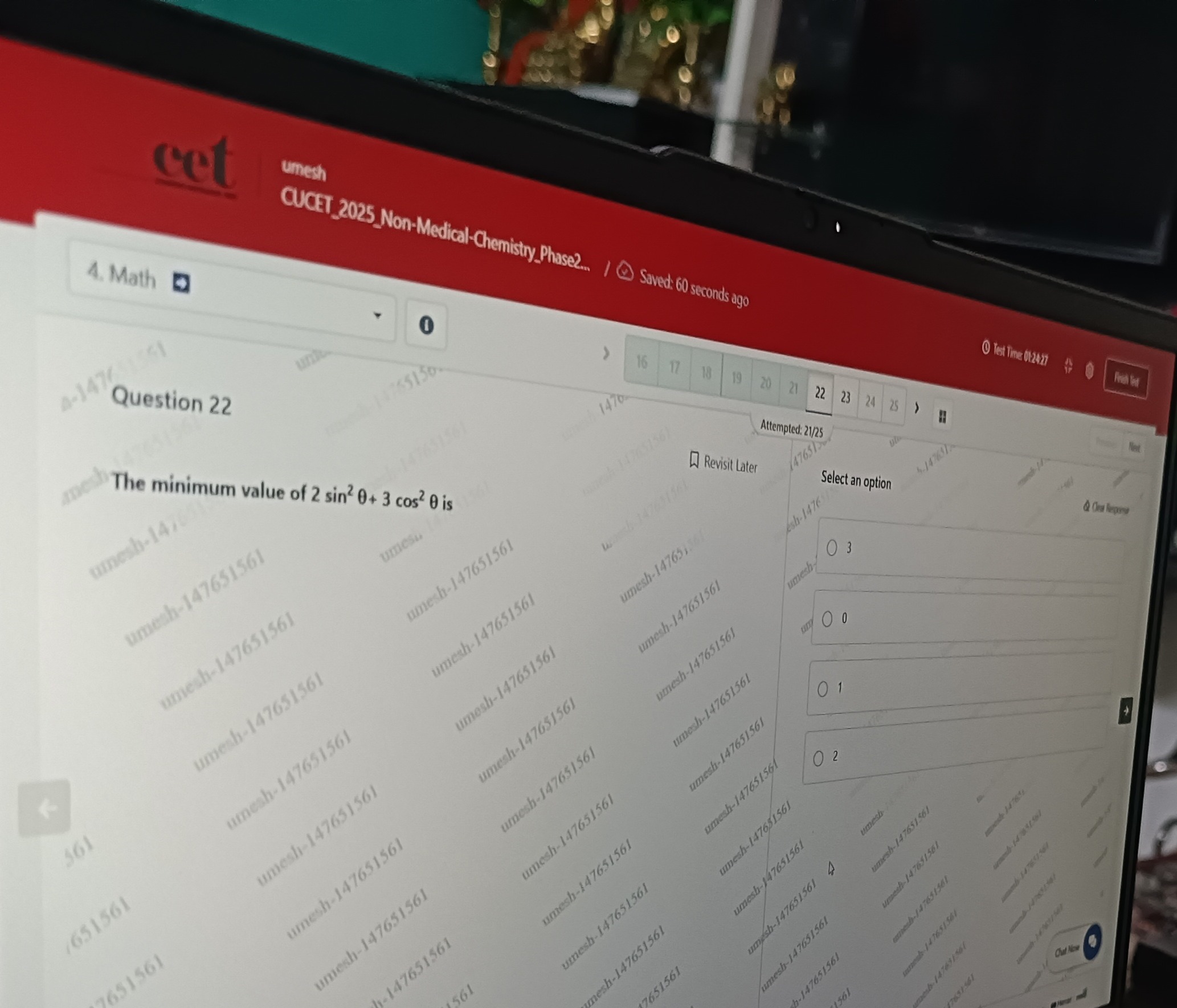
The minimum value of 2sin2θ+3cos2θ is
A
3
B
0
C
1
D
2
Answer
2
Explanation
Solution
The expression 2sin2θ+3cos2θ can be rewritten as 2sin2θ+3(1−sin2θ)=2sin2θ+3−3sin2θ=3−sin2θ.
Since 0≤sin2θ≤1, to find the minimum value of 3−sin2θ, we must subtract the maximum possible value of sin2θ, which is 1.
So, the minimum value is 3−1=2.
