Question

The system $N_2O_4 \rightleftharpoons 2NO_2$ maintained in a closed vessel at 60°C & a pressure of 5 atm has an average (i.e. observed) molecular weight of 69. At what pressure (in atm) at the same temperature would the observed molecular weight be (230/3)?

Answer 1

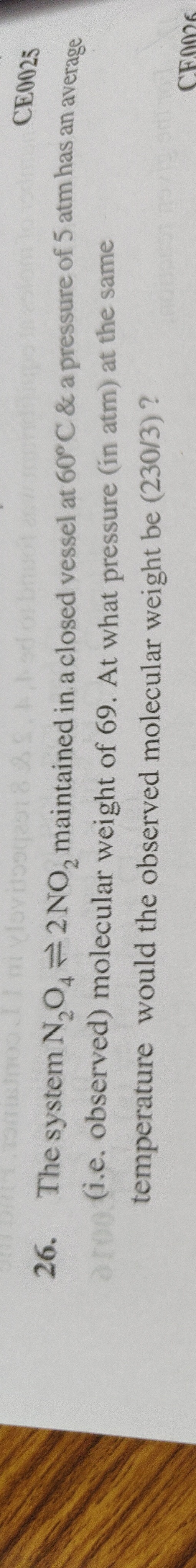
4.5 atm

Answer 2

For the dissociation $N_2O_4 \rightleftharpoons 2NO_2$, the theoretical molecular weight of $N_2O_4$ is $M_{theory} = 92$ g/mol. The observed molecular weight ($M_{obs}$) is related to the degree of dissociation ($\alpha$) by the formula $M_{obs} = \frac{M_{theory}}{1 + (n-1)\alpha}$. For this reaction, $n=2$, so $M_{obs} = \frac{M_{theory}}{1 + \alpha}$. This implies $1+\alpha = \frac{M_{theory}}{M_{obs}}$. In a closed vessel at constant temperature, the pressure ($P$) is directly proportional to the total number of moles, which is $n_{total} = n_0(1+\alpha)$. Thus, $P \propto (1+\alpha)$. Combining these, we get $\frac{P_1}{P_2} = \frac{1+\alpha_1}{1+\alpha_2} = \frac{M_{theory}/M_{obs,1}}{M_{theory}/M_{obs,2}} = \frac{M_{obs,2}}{M_{obs,1}}$. This simplifies to $P_1 M_{obs,1} = P_2 M_{obs,2}$. Using the given values, $5 \text{ atm} \times 69 \text{ g/mol} = P_2 \times \frac{230}{3} \text{ g/mol}$, which yields $P_2 = 4.5$ atm.