Question

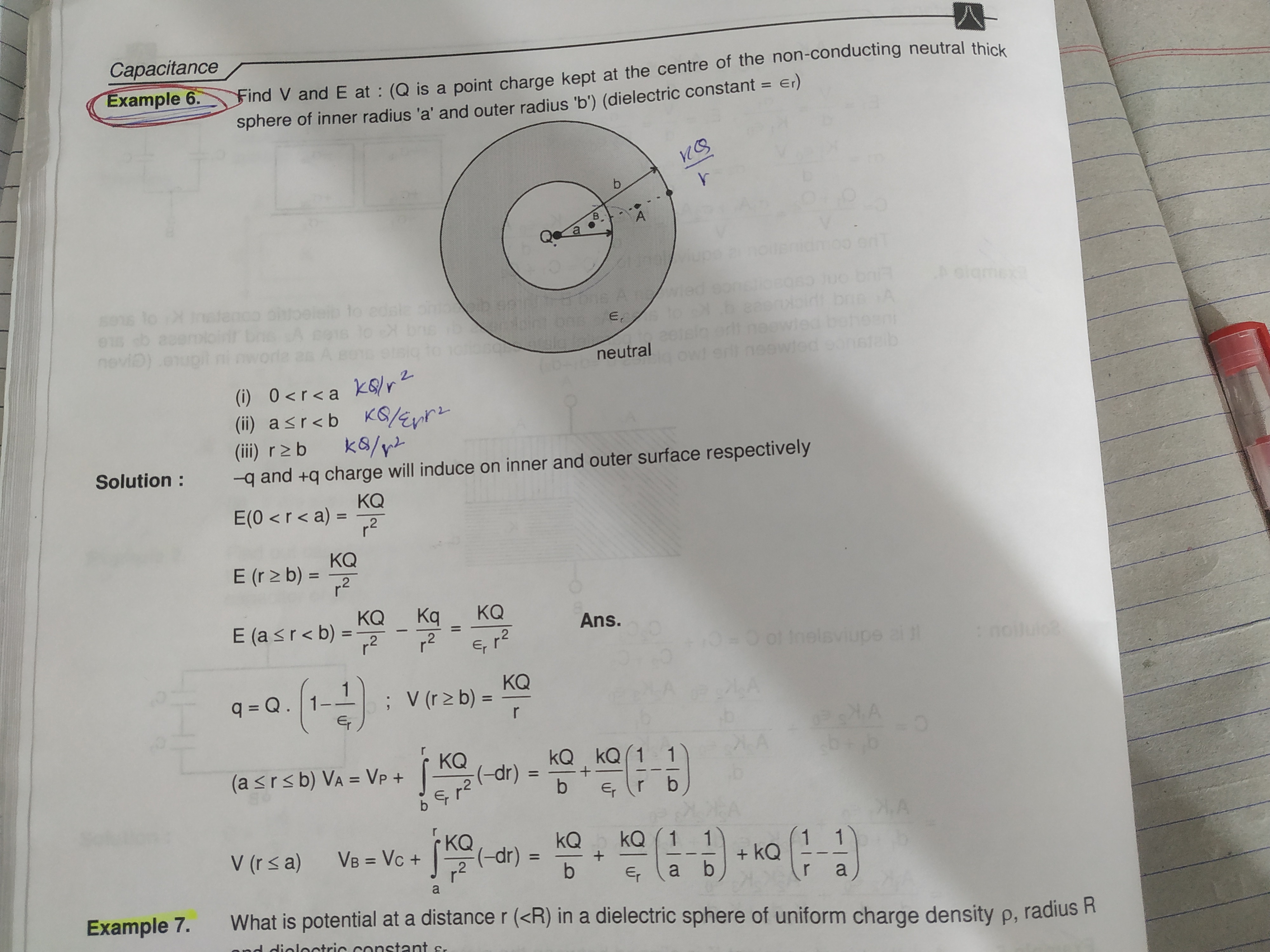
Find V and E at : (Q is a point charge kept at the centre of the non-conducting neutral thick sphere of inner radius 'a' and outer radius 'b') (dielectric constant = ∈r)

(i) 0<r<a (ii) a≤r<b (iii) r≥ b

Answer 1

E(0 < r < a) = $\frac{kQ}{r^2}$, E(a≤r<b) = $\frac{kQ}{∈_rr^2}$, E(r≥ b) = $\frac{kQ}{r^2}$

Answer 2

The electric field (E) and potential (V) are calculated for different regions around a thick non-conducting sphere with a central point charge Q.

Electric Field (E):

• Region $0 < r < a$ (Inside the inner cavity): By Gauss's Law, the electric field is $E = \frac{kQ}{r^2}$.
• Region $a \le r < b$ (Inside the dielectric): Considering the dielectric medium, $E = \frac{kQ}{\epsilon_r r^2}$.
• Region $r \ge b$ (Outside the sphere): By Gauss's Law, the electric field is $E = \frac{kQ}{r^2}$.

Induced Charge (q):

• The induced charge on the inner surface is $-q$ and on the outer surface is $+q$. The magnitude is $q = Q(1 - \frac{1}{\epsilon_r})$.

Electric Potential (V):

• Region $r \ge b$ (Outside the sphere): Integrating E from infinity, $V(r) = \frac{kQ}{r}$.
• Region $a \le r < b$ (Inside the dielectric): Integrating from $r=b$ inwards, $V(r) = V(b) + \int_{b}^{r} E dr' = \frac{kQ}{b} + \int_{b}^{r} \frac{kQ}{\epsilon_r r'^2} dr' = \frac{kQ}{b} + \frac{kQ}{\epsilon_r}(\frac{1}{r} - \frac{1}{b})$.
• Region $0 < r < a$ (Inside the inner cavity): Integrating from $r=a$ inwards, $V(r) = V(a) + \int_{a}^{r} E dr' = [\frac{kQ}{b} + \frac{kQ}{\epsilon_r}(\frac{1}{a} - \frac{1}{b})] + \int_{a}^{r} \frac{kQ}{r'^2} dr' = \frac{kQ}{b} + \frac{kQ}{\epsilon_r}(\frac{1}{a} - \frac{1}{b}) + kQ (\frac{1}{r} - \frac{1}{a})$.