Question
Question: Can you solve this question using series? (Do not involve Lhospital rule anywhere) $\Rightarrow \li...
Can you solve this question using series? (Do not involve Lhospital rule anywhere)
⇒limx→18(cos(ln(2cosx6π)))(arctan18x−4π)21
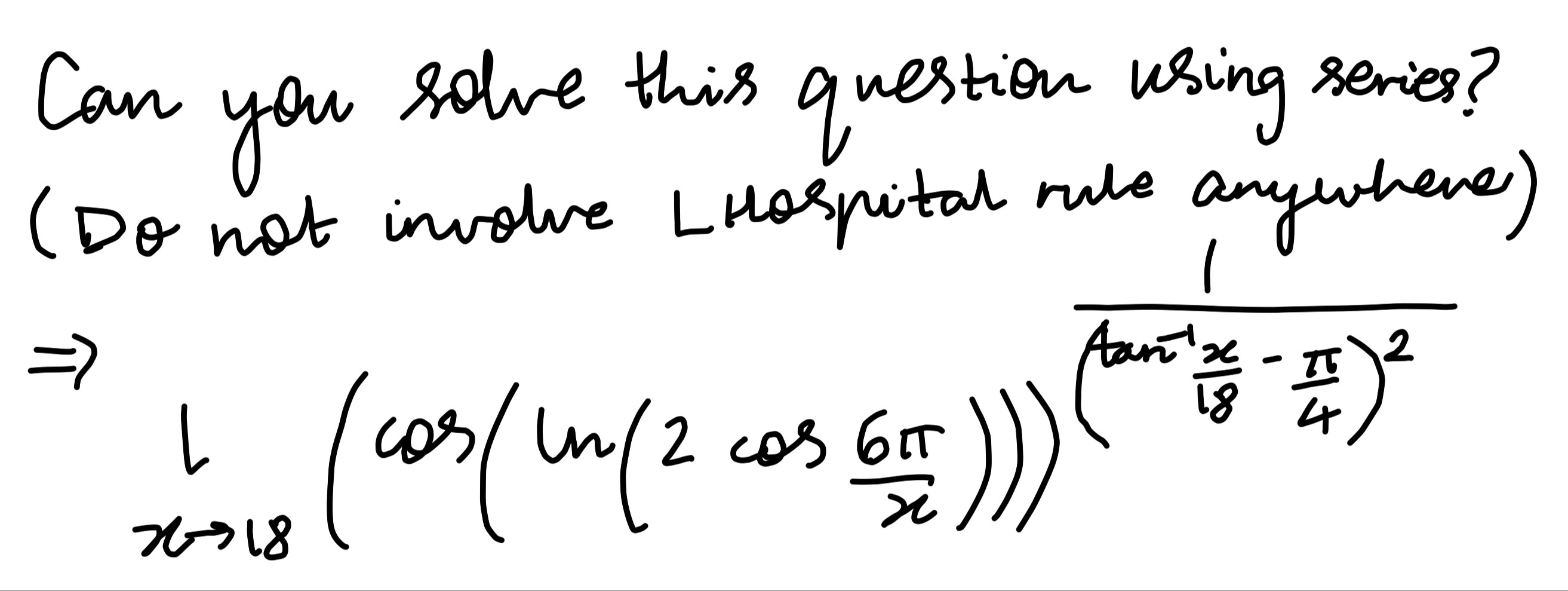
e−32π2
Solution
The limit is of the form 1∞, which is converted to elimx→ag(x)(f(x)−1). Let x=18+y, so y→0.
-
Expand (arctan18x−4π)2 using Taylor series for arctan(1+u) around u=0. This gives 1296y2(1−18y+O(y2)).
-
Expand cos(ln(2cosx6π))−1.
a. Expand x6π as 3π+δ, where δ=−54πy+O(y2). b. Expand 2cos(3π+δ) using cos(3π+δ)=21cosδ−23sinδ and series for sinδ,cosδ. This gives 1−3δ−2δ2+O(δ3). c. Expand ln(2cost) using ln(1+M)=M−2M2+O(M3). This gives −3δ−2δ2+O(δ3). d. Substitute δ in terms of y into ln(2cost). This gives 543πy+O(y2). e. Expand cos(Z)−1 using cosZ−1=−2Z2+O(Z4), where Z=ln(2cost). This gives −1944π2y2+O(y3).
-
Multiply the series expansions of g(x) and (f(x)−1) and take the limit as y→0.
The limit of the exponent simplifies to −32π2. The final answer is e−32π2.
