Question

Can someone please help me explain how to use the measures of right triangle to calculate the exact value of $\sin {30^ \circ }$? how can this information be used to determine the exact value of $\sin {60^ \circ }$?

Answer 1

We know that the right triangle has a side named hypotenuse and remaining two sides are base and height respectively. We also know the sin function is the ratio of opposite side to hypotenuses. This much data will help us to determine the values of sin function of $\sin {30^ \circ }$ and $\sin {60^ \circ }$.

Complete step by step solution:
First, we will draw a right triangle.

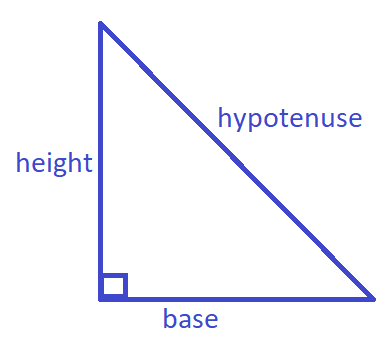
Now we have the diagram of the right triangle in front of us with one of the angles as the right angle and remaining two angles as either ${60^ \circ }$or ${30^ \circ }$.
Now let’s draw the both cases and the ratios of the angles.

Case 1:	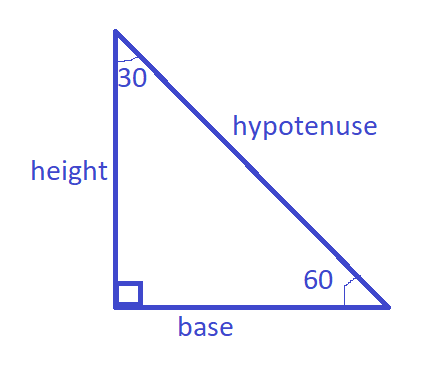Case 2: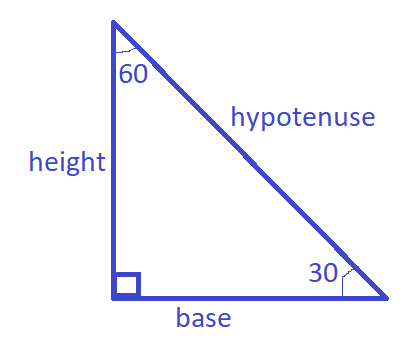
\sin {30^ \circ } = \dfrac{{opp}}{{hypt}} = \dfrac{{base}}{{hypt}}$$$$\sin {60^ \circ } = \dfrac{{opp}}{{hypt}} = \dfrac{{height}}{{hypt}}	\sin {30^ \circ } = \dfrac{{opp}}{{hypt}} = \dfrac{{height}}{{hypt}}$$$$\sin {60^ \circ } = \dfrac{{opp}}{{hypt}} = \dfrac{{base}}{{hypt}}

Thus in this way we found the ratio for both the angles. Now just putting the values of them we can get the answer.

Note: Note that we noted two cases above since the angle position is not mentioned. If it is given then use one of the situations that matches with one of the above. Also note that sin function is always the ratio of opposite side to hypotenuse but as the angle changes the value may change according to the angle so given.