Question

Can a physical quantity have units but still be dimensionless$?$

Answer 1

We know that physical quantities that are measured in base units or simple physical units can demonstrate the reason for the physical quantity of units, but are still dimensionless by using A substance which by calculation can be quantified. A unit is a standard of reference for physical quantity calculation.
Formula used:
The unit of dimension,
Angular displacement: Radian
Refractive index: Kilometres per second.

Complete step-by-step solution:
Given by,
We find the physical quantity has units,
Yeah, other quantities are dimensionless, but they have a unit.
The radian, for instance, is the unit for an angle. But it is dimensionless since the ratio of two lengths is known as being.
Meter, second, kilograms, kelvin, candela, moles, ampere will always be independent of the base units and a dimensionless number.
Additional examples:
angle, loudness, solid angles
Solid angle:
A solid angle is a 3D angular volume defined analogously to the two-dimensional concept of a plane angle. As shown below, a plane angle, consisting of the lines from two points meeting at a vertex, is described by the arc length of a circle subtended by the lines and by the radius of that circle.

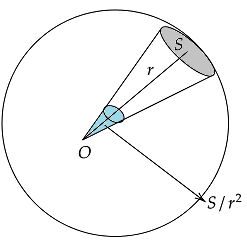
Here, In SI base units is ${m^2}$
Other units: Square degree
Hence,
The answer is Yes,
There are such unit quantities, but dimensional quantities.

Note: The dimension quantity with one as a quantity that is not associated with any physical dimension. With dimension one, it is a pure number. In Maths and Physics, these dimensionless quantities are regularly used. Such quantities are obtained as goods or quantity ratios.