Question

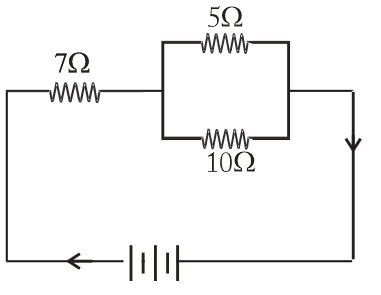
Calculate total resistance, total current and potential difference across $7\Omega$ resistor.

Answer 1

In order to solve the above problem, first see which resistance is connected in series or parallel and put the values in following formulas we will get the total resistance of the circuit.
For series ${R_{eqn}} = {R_1} + {R_2} + {R_3} +.. ...$
For parallel $\dfrac{1}{{{R_{eqn}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} +.. ...$
After then assume total potential difference is V and put the value of V and total resistance in the following expression we will get total current.
$I = \dfrac{V}{R}$
After this, put the value of current and resistance we will get a desired solution.

Complete step by step answer:
From the diagram it is clear that $5\Omega$ and $10\Omega$ resistances are connected in parallel and both are connected with $7\Omega$ in series. So, we can write total resistance is
Let
${R_1} = 5\Omega$
${R_2} = 10\Omega$
${R_3} = 7\Omega$
${R_{total}} = {R_3} + \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$
$= 7 + \dfrac{{5 \times 10}}{{5 + 10}}$
$= 7 + \dfrac{{50}}{{15}}$
$= \dfrac{{(7 \times 15) + 50}}{{15}}$
$= \dfrac{{155}}{{15}}$
${R_{total}} = 10.33\Omega$
Let the applied voltage be V.
So, according to ohm’s law
$V = IR$
$\implies I = \dfrac{V}{R}$
$\implies {R_{total}} = 10.33\Omega$
$\implies I = \dfrac{V}{{10.33}}$
$\implies I = 0.09680Vamp$
So, the potential difference across $7\Omega$ resistor as
$V' = (I)(7\Omega )$
$\implies V' = \dfrac{{0.9680V}}{7}$
$\therefore V' = 0.01380V$

Hence the potential difference across $7\Omega$ resistor is $0.0138$ time of total voltage applied.

Note:
Many times students may get confused between current and voltage concepts in series and parallel combination.
In series combination, the value of current in each resistance is the same.
In parallel combination, the potential difference in voltage across each resistance is the same.