Question

Calculate the ‘x’ in $M{n^{ + x}}$ if $\mu$ = 3.87 BM:-
A. 2
B. 3
C. 4
D. 5

Answer 1

given this question we have magnetic moment($\mu$)=3.87. So in the first stage we will calculate the number of electrons required to get 3.87 BM amount of magnetic moment. After that we will make electronic configuration of manganese. After that step we will again set the charge of ions on the manganese.

Complete answer:
We all know that the formula for the magnetic moment is: $\sqrt {n(n + 2)}$ , where n=number of unpaired electrons in the configuration of the atom or ion.
Mathematically, $\mu = \sqrt {n(n + 2)}$-(I)
Now putting the value of $\mu$ in the given equation.
So,$
3.87 = \sqrt {n(n + 2)} \\

$Now squaring the both side in the above equation:$
15 = n(n + 2) \\
{n^2} + 2n - 15 = 0 \\

$On solving this quadratic equation: We get,$
{n^2} + 5n - 3n - 15 = 0 \\
n(n + 5) - 3(n + 5) = 0 \\
n = 3,n = - 5
$$\therefore $n is the number of unpaired electrons in the ion so it can not be a negative number because the number of electrons can`t be negative. Hence , n=3 Now we have got the number of electrons in the ion is 3. Now we will make electronic configuration of manganese As we all know that atomic number of manganese is 25 So electronic configuration, Mn(25)=$1{s^2},2{s^2},2{p^6},3{s^2},3{p^6},4{s^2},3{d^5}$ Now we have to arrange the electronic configuration of manganese such that its configuration have 3 unpaired electrons in the valence shell So, we have to release 4 electrons from the manganese to get 3 unpaired electrons in the valence shell Therefore, electronic configuration will be:$M{n^{ + 4}}(21) = 1{s^2},2{s^2},2{p^6},3{s^2},3{p^{^6}},3{d^3}$

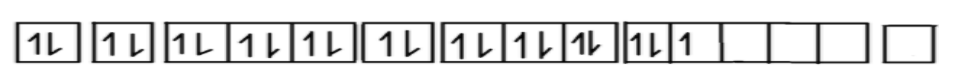
Now we can see in the configuration we have 3 electrons in the valence shell of manganese ions.
So value of x will be 4 in the given question.

**Therefore, the correct answer will be option number C.

Note:**
Magnetic moment is the property of a magnet that spreads the magnetic field to attract the material it provides mechanical moment to attract materials. Magnetic moment is also called that it is the strength of a magnet by which it attracts the other materials.