Question

Calculate the work done in taking a charge $- 2 \times {10^{ - 9}}C$ from A and B via C (in diagram).

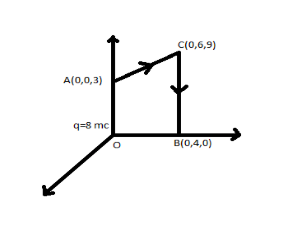
A. 0.2 J
B. 1.2 J
C. 2.2 J
D. Zero

Answer 1

To calculate the work done in moving the charge from point A to point B firstly, calculate the potential at the point A and B respectively. Then, calculate the potential difference between the point A and B created due to charge present at the origin. At last multiply the calculated potential difference with the charge moving from point A and B.

Formula used : $W = {q_1}\left( {{V_B} - {V_A}} \right)$
Here, $q_1$ is the charge which moves. ${V_B}$ is the potential at B due to q and ${V_A}$ is the potential at A due to q.

Complete step by step answer:
In this question, we want to find out the work done in bringing a charge $- 2 \times {10^{ - 9}}C$ from A to B via C. But as we know that moving a charge in electric field is independent of path chosen to move the charge in electric field and depends only on electric potential difference between them.

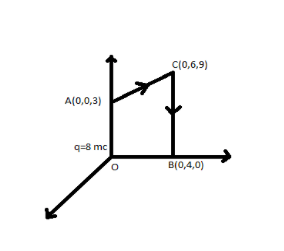
If charge directly moves from A to B then the result will be the same.

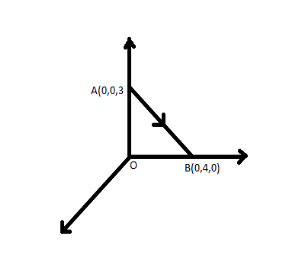
The only thing we need to do is to find the potential at A due to charge $q = 8mc$ at the origin i.e., .
${r_{OA}} =$ Distance between origin and the point $A = 3cm$.
Similarly, potential at B due to charge, $q = 8mc$at the origin

${r_{OB}} =$ Distance between origin and the point $B = 4cm$.
$\therefore work\;done = {q_1}\left( {{V_B} - {V_A}} \right)$
Now, by substituting the values we get,

Now, putting all the values,
${q_1} = - 2 \times {10^{ - 9}}C$
$q = 8mc = 8 \times {10^{ - 3}}C$

${r_{OB}} = 4cm$
${r_{OA}} = 3cm$
$W = - 2 \times {10^{ - 9}} \times 8 \times {10^{ - 3}} \times 9 \times {10^9}\left( {\dfrac{1}{4} - \dfrac{1}{3}} \right)$
$\;\therefore W = 1.27{\text{ }}J\;$ (Answer)

Note: Charge which is moving from one point to another is always multiplied to potential difference between the points, whatever the path of charge will be.