Question

Calculate the work done in raising a stone of mass 6 kg of specific gravity 2, immersed in water from a depth of 4m to 1m below the surface of water (g =10$m{{s}^{-2}}$).

Answer 1

This problem can be understood on the basis of Archimedes principle of buoyancy: "A body immersed in a liquid experiences an upward force due to the liquid, of a volume equal to the weight of the displaced liquid." The specific gravity given in the question represents the weight or density of a liquid as compared to the density of an equal volume of water.

Complete answer:
Due to the buoyant force, the net weight of the stone in the water will be different from the mass of the stone in the air. According to buoyancy, the net weight of the stone in the liquid is ρV, where ρ is the mass density of the liquid and V is the volume of the immersed body.
Using the value of specific gravity, the weight of the stone that will be lost in the water is given as:
${{m}^{'}}=\dfrac{weight\text{ in air}}{specific\text{ gravity}}=\dfrac{6}{2}$= 3Kg
Hence, weight of stone in the water will be: 6 – 3 = 3 Kg

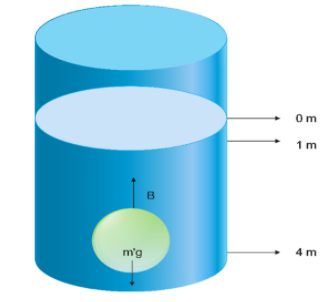
The equation of motion in this case, shown in figure, is:
F = m'g
Where g is the gravity, 10 $ms^{-2}$.
The work done will be: Force × Displacement:
W = m'g (h-h')
= 3 × 10 × 3
=$90kg{{m}^{2}}{{s}^{-2}}$
Hence, the work done in moving a stone immersed in water from depth of 4 m to 3m below the surface of water is 90 J.

Note:
The body is less dense than water. If it is pushed upwards from position A to position B, water must move downward. The volume of the body at position A will now be replaced with water, The net effect is that as the volume of the body moves from position A to position B, an equal volume of water moves from position B to position A.