Question

Calculate the unknown resistance $R$ of the circuit as shown in the figure, all resistance is connected in series. The current flowing through the circuit is $2A$ and the battery is of $20V$ voltage.

(A) $1\Omega$
(B) $2\Omega$
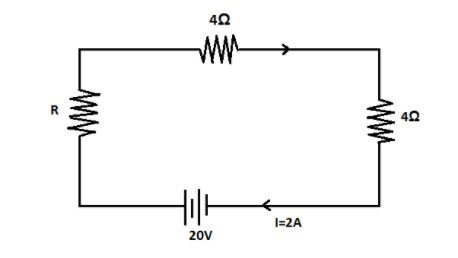
(C) $4\Omega$
(D) $6\Omega$
(E) $12\Omega$

Answer 1

Resistors can be connected in two different ways. One is the parallel connection and the other is a series connection. Here we have a circuit where the three resistors are connected in series. We are given the values of the two resistors, the voltage of the circuit and the total current flowing through the circuit. Now with all these values, we have to find the value of the third resistor$R$.
Formula used
$V = IR$(Where $V$stands for the voltage of the circuit, $I$stands for the current flowing through the circuit, and $R$stands for the total resistance of the circuit)

Complete step by step solution:
In the question, it is given that
The voltage is $V = 20Volts$
The current flowing through the circuit is given by,
$I = 2A$
Since the resistors are connected in series the total equivalent resistance of the circuit will be the sum of individual resistances of the circuit. It is given that the other two resistors of the circuit have a resistance of $4\Omega$ each. Hence we can write the equivalent resistance of the circuit as,
${R_{eq}} = R + 4\Omega + 4\Omega$
$\Rightarrow {R_{eq}} = R + 8\Omega$
According to Ohm’s law, the voltage is given by,
$V = IR$
Here we have to put the equivalent resistance of the circuit in the above equation,
$V = I{R_{eq}}$
We know that the voltage $V = 20V$, current,$I = 2A$and The equivalent resistance${R_{eq}} = R + 8$
Substituting these values in the equation for voltage we get,
$20 = 2\left( {R + 8} \right)$
Opening the bracket, we get
$20 = 2R + 16$
Solving the equation, we get
$20 - 16 = 2R$
$\Rightarrow 2R = 4$
From this, we get the value of the resistor $R$as,
$R = \dfrac{4}{2} = 2\Omega$

The answer is: Option (B): $2\Omega$

Note:
If the resistors in a circuit have an end to end connection, they are said to be in a series connection. If all the resistors in a circuit are connected to two common points then they are said to be in a parallel connection. In a series connection, the current flowing through all the resistors will be the same. In a parallel connection, the potential difference between all the resistors will be the same.