Question

Calculate the tension in the string shown in figure . The pulley and the string are light and all surfaces are frictionless . Take $g = 10m/{s^2}$

Answer 1

First, the diagram should be completed by introducing the places where the tensions are worked.
Second, find the equations of motions for the two blocks individually. Note that the blocks will move with an acceleration. Finally, add the two equations and find the tension of the string.

Formula used:
Let the mass of each block is $m$. Block-2 is hanging with a string and Block-1 is kept on the surface.
And the acceleration is $a$ .
If the tension of the string is $T$
The equation of motion for the Block-1 is, $T = ma$
And, The equation of motion for the Block-2 is, $T + ma = mg$

Complete step by step answer:

The above figure is showing that two blocks are attached with a string in a pulley. The tension of the string has to be calculated. The figure can be modified:

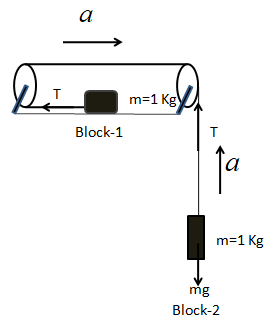
Let the mass of each block is $m = 1kg$.
Block-1 is kept in the frictionless surface attached with the string and is moving with an acceleration $a$.
Block-2 is hanging with a string attached with the pulley and is moving upwards with the acceleration $a$. The weight of the Block-2 is acting downwards.
The tension $T$ is shown in the picture.
The equation of motion for the Block-1 is, $T = ma$
And, The equation of motion for the Block-2 is, $T + ma = mg$
By adding the two equations we get,
$2T + ma = ma + mg$
$\Rightarrow 2T = mg$
$\Rightarrow T = \dfrac{{1 \times 10}}{2}$
$\Rightarrow T = 5N$

Note: If the two masses are different i.e $m$and $M$ then the formula of the tension for this type of problem will be,
$T = m\dfrac{M}{{m + M}}g$
$\Rightarrow T = \dfrac{M}{{1 + \dfrac{M}{m}}}g$
Since, $\dfrac{M}{{1 + \dfrac{M}{m}}} < M$
Hence, $T < Mg$
So, the tension will be less than the weight of the mass $M$.