Question

Calculate the smaller force if the bigger force is $40N$ and the resultant force is perpendicular to the smaller force. The two forces are acting at an angle of ${120^0}$.

Answer 1

Vectors add according to the triangle law or equivalent parallelogram. Let the resultant force be $R$. This vector is making a right angle with a smaller force${\vec F_1}$. This implies that the resultant makes an angle ${30^0}$ with a bigger force ${\vec F_2}$.
Diagram:

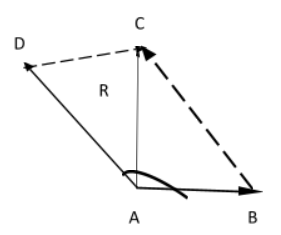
Complete answer:
Let the smaller force be represented by ${\vec F_1}$ and the bigger force be represented by ${\vec F_2}$
From the right angle triangle ACD, defining $\sin \alpha$ we get
$\sin \alpha = \dfrac{{{\text{Opposite}}}}{{Adjacent}} = \dfrac{{DC}}{{AD}}$
We know that $AD$=${\vec F_2}$=$40N$
The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. Also opposite sides of the parallelogram are equal. Therefore
$DC$=$AB$=${\vec F_1}$=?
By parallelogram law of vectors, the resultant force be represented by ${\vec F_R}$
We know that $\left| \\!{\underline {\, {DAB} \,}} \right. = {120^0}$, therefore

{DAC} \,}} \right. = {120^0} - {90^0} = {30^0}$$ $$\sin {30^0} = \dfrac{{{{\vec F}_1}}}{{{{\vec F}_2}}}$$ $${\vec F_1}$$=$$\sin {30^0} \times {\vec F_2}$$ $${F_1} = \dfrac{1}{2} \times 40$$ $${F_1} = 20N$$ **Therefore the smaller force is $$20N$$.** **Note:** This problem may also be solved using another method. Let there be two vectors $$\vec A{\text{ and }}\vec B$$ Let the angle $$\theta = {120^0}$$ between the two vectors. We know the resultant force formula as $$R.F = \sqrt[2]{{{F_1}^2 + {F_2}^2 + 2{F_1}{F_2}\cos \theta }}$$ Here, $$R.F$$ is the resulting force $${F_1}$$ and $${F_2}$$ are the known two forces $$\theta $$ is the angle between the two forces. $${\left| {RF} \right|^2} = {\left| A \right|^2} + {\left| B \right|^2} + 2AB\cos \theta $$ Let A be the bigger force and B be the smaller force. We know that $$\theta = {120^0}$$, substituting in the above formula, Value for $$\cos {120^0} = - \dfrac{1}{2}$$, $$R{F^2} = {A^2} + {B^2} - AB$$ Given that the resultant makes a right angle with the smaller force So $$B = - A\cos \theta $$---- (1) Substituting the known values that are, $${\rm A} = 40{\rm N}$$ $$\theta = 12{0^0}$$ Substituting in equation 1 we get, $$B = - 40 \times - \dfrac{1}{2}$$ $$B = 20N$$ Thus we can also use this method to find the smaller force.