Solveeit Logo
Login

Question

Question: Calculate the resultant force, when four forces of \(30\;N\) due to east, \(20\;N\)due to north, \(5...

Calculate the resultant force, when four forces of 30  N30\;N due to east, 20  N20\;Ndue to north, 50  N50\;N due to west and 40  N40\;N due to south, are acted upon by a body.
(A) 202N20\sqrt 2 N, 60∘{60^\circ }, south-west
(B) 202N20\sqrt 2 N, 45∘{45^\circ }, south-west
(C) 202N20\sqrt 2 N, 45∘{45^\circ }, north-east
(D) 202N20\sqrt 2 N, 45∘{45^\circ }, south-east

Explanation

Solution

Here given that the four forces are acting on the object from four directions. To solve this question we will use the concept of cardinal directions, we will consider the north as +y + y axis while the south as −y - y axis, similarly use will consider the west as −x - x axis while east as +x + x axis. Hence we will evaluate the resultant vectors of the forces from all the directions by using the vector sum property.

Formula used:
Resultant force by vector sum property
⇒R⃗=F⃗1+F⃗2+F⃗3+...\Rightarrow \vec R = {\vec F_1} + {\vec F_2} + {\vec F_3} + ...
The angle between two vectors with a common origin
⇒tan⁡θ=FyFx\Rightarrow \tan \theta = \dfrac{{{F_y}}}{{{F_x}}}

Complete step by step solution:
From the given terms the following figure can be concluded.

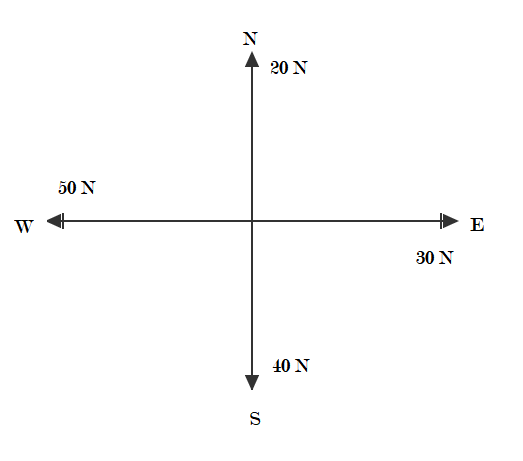
We will evaluate the resultant force by using the vector sum property by using graphical representation as shown

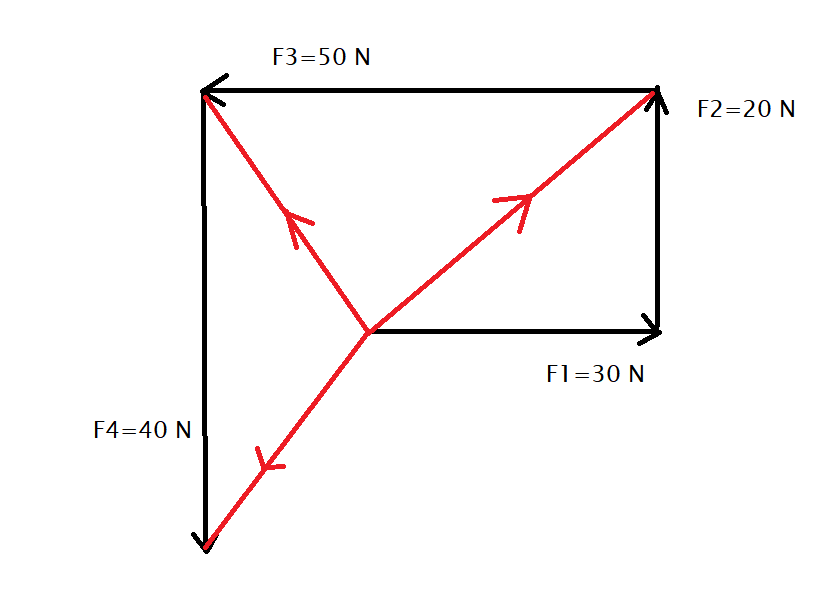
Hence from the above figure, we can see that the forces can be given in the form of vector components such as
⇒F⃗1=30i^N\Rightarrow {\vec F_1} = 30\hat iN
⇒F⃗2=20j^N\Rightarrow {\vec F_2} = 20\hat jN
⇒F⃗3=−50i^N\Rightarrow {\vec F_3} = - 50\hat iN
⇒F⃗4=−40j^N\Rightarrow {\vec F_4} = - 40\hat jN
Now using the vector sum properties we will evaluate the resultant force as R⃗\vec Rhence given as
⇒R⃗=F⃗1+F⃗2+F⃗3+F⃗4\Rightarrow \vec R = {\vec F_1} + {\vec F_2} + {\vec F_3} + {\vec F_4}
⇒R⃗=30i^N+20j^N+(−50i^N−40j^N)\Rightarrow \vec R = 30\hat iN + 20\hat jN + \left( { - 50\hat iN - 40\hat jN} \right)
Now evaluating the sum of vectors results in
⇒R⃗=−20i^N−20j^N\Rightarrow \vec R = - 20\hat iN - 20\hat jN
⇒R⃗=−20N(i^+j^)\Rightarrow \vec R = - 20N\left( {\hat i + \hat j} \right) …………(1)(1)
Now we will evaluate the magnitude of the resultant by ∣R∣\left| {\left. R \right|} \right..
⇒∣R∣=(−20N)2(i^2+j^2)\Rightarrow \left| R \right| = \sqrt {{{\left( { - 20N} \right)}^2}\left( {{{\hat i}^2} + {{\hat j}^2}} \right)}
∴R=202N\therefore R = 20\sqrt 2 N
Therefore the resultant value of the force on the body is given as R=202NR = 20\sqrt 2 N.
Now we conclude that from the equation (1)(1) that the direction of the resultant force can be given as

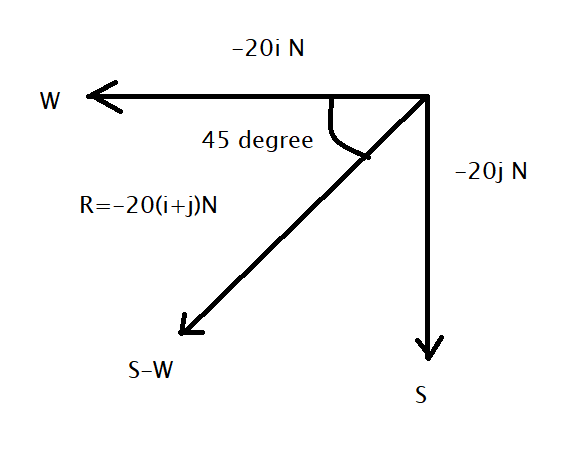
Hence the direction of the resultant force concluded from a figure that is the south-west. The angle of the resultant force can be given as
⇒tan⁡θ=FyFx\Rightarrow \tan \theta = \dfrac{{{F_y}}}{{{F_x}}}
⇒tan⁡θ=−20−20\Rightarrow \tan \theta = \dfrac{{ - 20}}{{ - 20}}
⇒tan⁡θ=1\Rightarrow \tan \theta = 1
Hence the angle is given by the inverse of tan⁡θ\tan \theta such as
⇒θ=tan⁡−11\Rightarrow \theta = {\tan ^{ - 1}}1
∴θ=45∘\therefore \theta = {45^\circ }
Therefore the resultant force acting on the body is R=202NR = 20\sqrt 2 N at an angle of 45∘{45^\circ } in the south-west direction.
Hence the correct answer is option (B) 202N20\sqrt 2 N, 45∘{45^\circ }, south-west is.

Note:
When several forces act on a point, then their sum can be evaluated by using the rules of vector algebra. For the sum of forces acting we can use the triangular method as well as the parallelogram method. Here in this question, we have used the triangular method.