Question
Question: Calculate the relative acceleration of \(A\) with respect to \(B\) if \(B\) is moving with accelerat...
Calculate the relative acceleration of A with respect to B if B is moving with acceleration a0 towards the right.
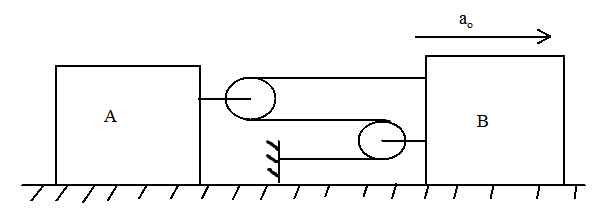
Solution
First calculate the tensions in all the strings in the figure. Then use the formula which relates tension in string and object’s acceleration to calculate the acceleration of A in terms of acceleration of B. After this is done, we have the acceleration of both the bodies. Subtract accordingly to get the acceleration of A with respect to B .
Formulas Used:
∑Taicosθ=0
Where, T is the tension in the string attached to an object, ai is the acceleration of the ith object and θ is the angle between the directions of tension and acceleration of an object.
Complete step by step answer:
First, we will calculate the tension in all the strings. We start from the top. Let the string at the top have a tension T towards the object B. Therefore, the 3rd string from the top, which connects the two pulleys together will also have a tension T in the same direction and similarly, the string at the bottom will also have a tension T. Now, the string attached to A is experiencing tension from two strings, therefore the tension in this string will be the sum of these two strings i.e. this string will have a tension of 2T in the same direction. The same is the case with the lower string attached to B. Tension in this string will also be equal to 2T.
Since tension is always applied away from the body, the same will be the case here. These pulleys/strings do not have any velocity of their own, we can conclude that no net force is acting in them and these tensions are balanced. So, we assume that the same amount of force is acting on all the strings in opposite directions as the tensions we calculated above. The final diagram is shown below.
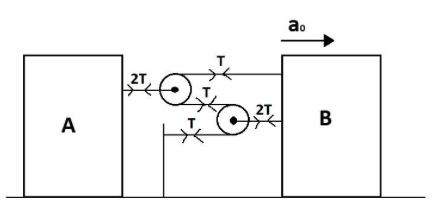
Now we use the formula ∑Taicosθ=0. For A, tension is 2T, let its acceleration be a1 and the angle between them will be 0∘ (tension is always applied away from the body). For B, tension is (2T+T)=3T, its acceleration is a0 (given) and the angle between them will be 180∘. Therefore, the formula becomes (2T×a1×cos0)+(3T×a0×cos180)=0
On solving this, we get 2Ta1−3Ta0=0
Transposing, 2Ta1=3Ta0 ⇒a1=23a0
Or, a1=1.5a0
We have the acceleration of A. The acceleration of B is a0. Therefore, relative acceleration of A will be a1−a0=1.5a0−a0=0.5a0 .
This is the required answer.
Note: Tension in a string is always applied away from the body it is attached to. If we do not balance the tension in the string it will mean that force is applied on the string and therefore, the string shall show motion in that direction which is not the case. Hence it is necessary to balance the tensions in the strings.
