Question

Calculate the ratio of the equivalent capacitance of the circuit when two identical capacitors are in series to that when they are in parallel.

& A.\dfrac{1}{4} \\\ & B.\dfrac{1}{2} \\\ & C.1 \\\ & D.2 \\\ & E.4 \\\ \end{aligned}$$

Answer 1

To find the ratio between the equivalent capacitances which are in series and in parallel connection, we need to find the individual values of the net capacitance due to series and parallel connection and then find the ratio between them.
Formula used:
$\dfrac{1}{C_{s}}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}$ and $C_{p}=C_{1}+C_{2}$

Complete answer:
A capacitor can store electrical energy, and behaves as a temporary battery. They are used mainly to maintain the power supply while batteries are being changed. It can also store information in the form of binary digits. It is the main component used in full wave and half wave rectifiers. (symbol: F), named after the English physicist Michael Faraday. A 1 farad capacitor, when charged with 1 coulomb of electrical charge, has a potential difference of 1 volt between its plates. The series of capacitors is the sum of reciprocal of its individual capacitors, whereas in resistance the parallel is the sum of reciprocal of its individual resistors. Also remember that capacitors can charge and discharge.
A capacitor is a two terminal component that stores electrical energy in the form of potential energy, and later discharges them. This property is called the capacitance of the capacitor.
Let us assume that the two capacitance are $C_{1}$ and $C_{2}$ since they are identical, we can say that $C_{1}=C_{2}=C$
The circuit diagram will be as follows:

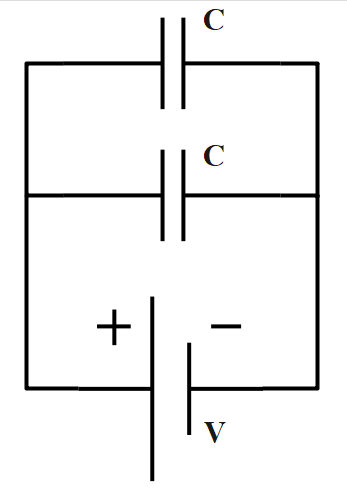
Let the net capacitance due to series be given as $C_{s}$ then, we know that $\dfrac{1}{C_{s}}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}=\dfrac{2}{C}$
$\implies C_{s}=\dfrac{C}{2}$
Similarly, the net capacitance due to parallel be given as $C_{p}$ then, we know that $C_{p}=C_{1}+C_{2}=2C$
Taking the ratio, we get, $\dfrac{C_{s}}{C_{p}}=\dfrac{\dfrac{C}{2}}{2C}=\dfrac{1}{4}$

So, the correct answer is “Option A”.

Note:
The series of capacitors is the sum of reciprocal of its individual capacitors, whereas in resistance the parallel is the sum of reciprocal of its individual resistors. Also remember that capacitors can charge and discharge.