Question

Calculate the rate of flow of glycerin of density $1.25 \times {10^3}kg/{m^3}$ through the conical section of a pipe if the radii of its ends are $0.1m$ & $0.04m$ and the pressure drop across its length is $10N/{m^2}$ .

Answer 1

Hint
To solve this question, we have to use the continuity equation and the Bernoulli’s equation. Then, using the formula for the rate of flow in terms of the area and the velocity, we can find it out.
Formula Used:
${A_1}{v_1} = {A_2}{v_2}$
${P_1} + \rho g{h_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \rho g{h_2} + \dfrac{1}{2}\rho {v_2}^2$
$Q = Av$ , here $Q$ is the rate of flow of a fluid through a section having area $A$ and velocity $v$
Here are ${A_1}$ and ${A_2}$ the areas, ${P_1}$ and ${P_2}$ the pressures, ${v_1}$ and ${v_2}$ the velocities, and ${h_1}$ and ${h_2}$ the heights of the section 1 and 2 of a pipe.

Complete step by step answer

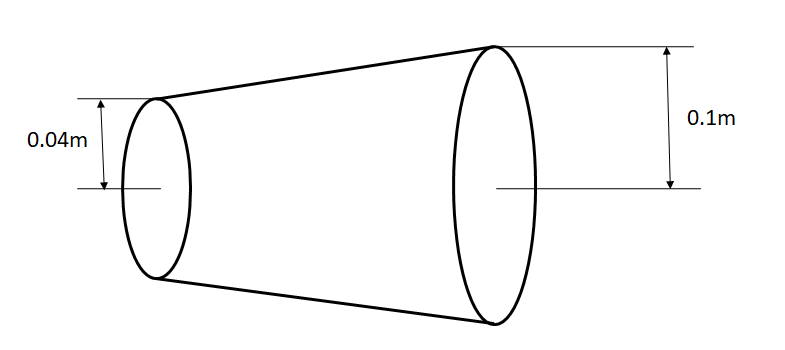
From the continuity equation we have
${A_1}{v_1} = {A_2}{v_2}$
$\pi {r_1}^2{v_1} = \pi {r_2}^2{v_2}$
Separating ${v_2}$ we get
${v_2} = {\left( {\dfrac{{{r_1}}}{{{r_2}}}} \right)^2}{v_1}$
According to the question, ${r_1} = 0.04m$ and ${r_2} = 0.1m$ . Putting these values, we get
${v_2} = {\left( {\dfrac{{0.04}}{{0.1}}} \right)^2}{v_1}$
${v_2} = 0.16{v_1}$ (1)
From the Bernoulli’s equation we have
${P_1} + \rho g{h_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \rho g{h_2} + \dfrac{1}{2}\rho {v_2}^2$
As the glycerin flows through the pipe which is horizontal, so we have ${h_1} = {h_2}$ , which gives
${P_1} + \rho g{h_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \rho g{h_1} + \dfrac{1}{2}\rho {v_2}^2$
Cancelling $\rho g{h_1}$ from both the sides, we have
${P_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \dfrac{1}{2}\rho {v_2}^2$
Substituting from (1)
${P_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \dfrac{1}{2}\rho {\left( {0.16{v_1}} \right)^2}$
On rearranging the terms, we have
${P_2} - {P_1} = \dfrac{1}{2}\rho {v_1}^2 - \dfrac{1}{2}\rho {\left( {0.16{v_1}} \right)^2}$
Taking $\dfrac{1}{2}\rho {v_1}^2$ common on the RHS
${P_2} - {P_1} = \dfrac{1}{2}\rho {v_1}^2\left( {1 - 0.0256} \right)$
${P_2} - {P_1} = 0.4872\rho {v_1}^2$
According to the question, ${P_2} - {P_1} = 10N/{m^2}$ , and $\rho = 1.25 \times {10^3}kg/{m^3}$ . So, we get
$10 = 0.4872 \times 1.25 \times {10^3} \times {v_1}^2$
${v_1}^2 = 0.01642$
On simplifying, we get
${v_1}^2 = 0.0164$
${v_1} = 0.128m/s$
Now we know that the rate of flow is given by
$Q = Av$
Taking the values at the section 1
$Q = {A_1}{v_1}$
$Q = \pi {r_1}^2{v_1}$
Substituting the values
$Q = \pi {\left( {0.04} \right)^2}\left( {0.128} \right)$
$Q = 6.43 \times {10^{ - 4}}{m^3}/s$
Hence, the rate of flow of glycerin through the given conical section of the pipe is equal to $6.43 \times {10^{ - 4}}{m^3}/s$ .

Note
Here in this question, we have not been given any information regarding the heights of the two sections of the conical pipe. So we assumed that the pipe should be horizontal. But this is not the case every time. A fluid can flow through the pipe having any configuration.