Question

Calculate the packing efficiency in simple cubic lattice?

Answer 1

Unit Cell
A unit cell is the most basic and least volume consuming repeating structure of any solid. It is used to visually simplify the crystalline patterns solids arrange themselves in. The entire space lattice is built by the repeating arrangement of unit cells. A unit cell is a geometric shape even by itself. It has three edges. And these three edges form three respective angles. The edges of a unit cell are as follows

Primitive Unit Cells
A primitive unit cell only has atoms, molecules or ions at the corners of the lattice. There are no particles located at any other position in a primitive unit cell. So essentially a primitive unit cell has only one lattice point.

Non-Primitive Unit Cells
In this type of unit cell, there are particles not only at the corners of the lattice but in other positions as well. These additional constituent particles are either on the face of the unit cell or inside the unit cell. So there is more than one lattice point in a non-primitive unit cell. There are actually three types of non-primitive unit cells, namely:

Body Centered: It has one particle at the center of the body. Other particles (one or more) are at the corner of the lattice

Face Centered: This contains particles on every face of the lattice and other particles on the corners end centered: Has particles at the corners and one particle at the center of the opposite faces.
The percentage of the total space filled by the particles in the three dimensional close packing is known as the packing efficiency.

Complete step by step answer:
In a simple cubic lattice the atoms are located only on the corner of the cube.The particles touch each other along the edge.

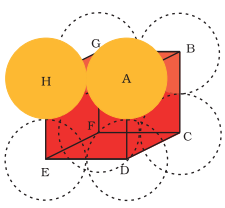
The edge length or side of the cube be 'a', and the radius of each particle be 'r'. $a=2r$
Volume of cube = ${{a}^{3}}$
${{(2r)}^{3}}=8{{r}^{3}}$
In simple cube, each unit cell has only one sphere, Volume of sphere = $\dfrac{4}{3}\pi {}^\text{3}$ Packing efficiency = $\dfrac{\mathbf{Volume}\text{ }\mathbf{of}\text{ }\mathbf{one}\text{ }\mathbf{atom}~~~~}{\mathbf{Volume}\text{ }\mathbf{of}\text{ }\mathbf{cubic}\text{ }\mathbf{unit}\text{ }\mathbf{cell}~}\times 100$ =$\dfrac{4/3\pi r{}^\text{3}}{8r{}^\text{3}}\times 100$
=$\dfrac{\pi }{6}\times 100$
=52.36% = 52.4%

A Frenkel defect is another form of a point defect which is created when an atom or cation leaves its original place in the lattice structure to create a vacancy while occupying another interstitial position within the solid crystal.And is also called dislocation defect.
Characteristic of Frenkel Defect
This defect occurs only when cations are smaller when compared to the anions. There are also no changes in chemical properties. There is also no significant impact of Frenkel defect on the density of the solid and therefore both the volume and mass of the solid is preserved. In such cases, substances also maintain their electrical neutrality.

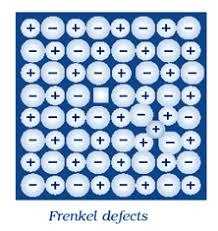
Examples
In order for the Frenkel defect to occur in an atom, it requires a low coordination number as well as having the crystal lattices open for the molecule. Frenkel defects are mostly exhibited in ionic solids where the smaller ion (usually the cation) is dislocated. Some examples include $AgBr,\text{ }ZnS,\text{ }AgCl$, and $AgI$ .
Silver Bromide,Zinc Sulfide,Silver Chloride,Silver Iodide
Here the defect occurs mainly due to the smaller size of $Z{{n}^{2+}}$ and $A{{g}^{+}}$ ions. Meanwhile, Silver Bromide also shows another form of point defect known as Schottky defects.

Note:
Most of the students get confused between Frenkel and Schottky defect so always remember the key differences
Key Differences Between Schottky and Frenkel Defect
An ionic material experiences both frenkel and schottky defects but there are some differences between them. We have listed the main ones below.

Schottky Defect	Frenkel Defect
In Schottky defects the difference in size between cation and anion is small.	Frenkel defect contains ionic crystals where the anion is larger than the cation.
Both anion and cation leave the solid crystal.	Usually the smaller ion cation leaves its original lattice structure.
Atoms permanently leave the crystal.	Atoms remain within the solid crystal.
There is formation of two vacancies.	Only one vacancy is created.
The density of the solid decreases.	Density remains the same.