Question

Calculate the number of atoms in a cubic based unit cell having one atom on each corner and two atoms on each body diagonal.

Answer 1

As we know, the atoms in a cubic based unit cell having one atom on each corner means there are $8$ atoms.
The contribution of corner atoms in each cubic cell is ${{y}_{8}}$.
Therefore,
Total no. of atoms $=8\times \dfrac{1}{8}=1$ on corner
There are $4$ diagonal in a cube and the atoms in a body diagonal are complete within the cubic cell.

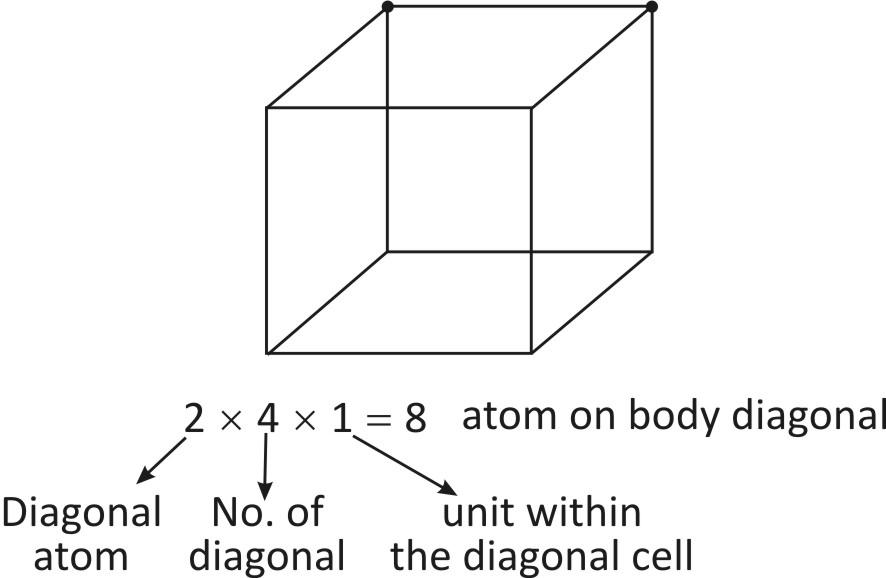
So, Total no. of atoms on unit cell $=8+1=9$ atoms.

Complete step by step answer:
-As we all know there are total seven different kinds of unit cells which are different in corresponding with the edges and the angles between them
-Each unit cell has six sides and each side is a parallelogram.
-As per the question asked here, we will focus on the cubic cell unit. In cubic unit cells, all sides are $90{}^\circ .$
-In a crystalline solid, there is a regular and repetitive arrangement of particles in three dimensions (a crystal lattice). We can represent the whole structure of the crystal by drawing the structure of the smallest identical unit when stacked together from the crystal.
-Basic repeating unit is called a unit cell, which forms the entire lattice.

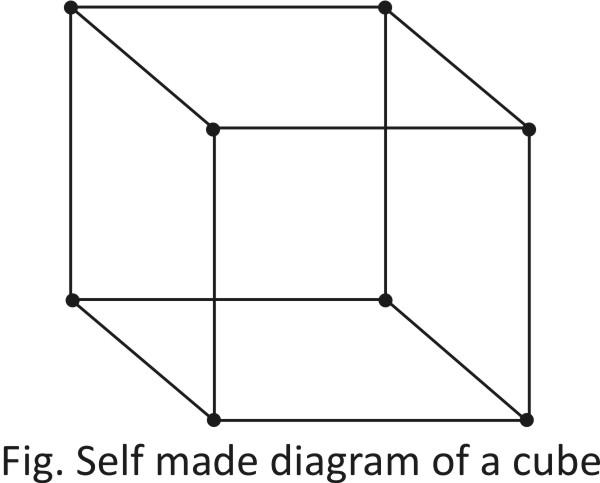
-As we can see here, there are a total $8$ atoms present at the corner.
-The contribution of corner atom in each cubic cell in $\dfrac{1}{8}.$
$\therefore$ Total no. of $=8\times \dfrac{1}{8}=1$ atoms on corner
-As we can see, there are $4{}^\circ$ diagonals in a cube. The atoms in a body diagonal are completely present within the body diagonal cells.
So, $2\times 4\times 1=8$ atoms on the body diagonal.
Therefore, to calculate the number of atoms in a cubic based unit cells having one atom at each corner and two atoms an each body diagram $=2\times 4+1$
$=8\times 1$
$=\mathbf{9}$
So, the answer is $9.$

Additional Information:
If the cubic unit cell contains eight component atoms or molecules placed at the corners of the cube, then it is called a simple cube.
The unit cell consists of an identical component in the centre of the cube then it is called a body centered cube (bcc).
The unit cell consists of an identical component at the centre of the each face in addition with the corners of the cube, then the unit cell is called as face centered cubic cell. (fcc).

Note:
The number of atoms in a primitive cubic unit cell is $1$
i.e., $\dfrac{1}{8}\times 8=1$
There are total $8$ atoms or molecules or ions present at the corners of a cube in a simple cubic unit cell.