Question
Question: Calculate the net inductance of the following circuit. Assume each inductor to be \( 1 \) henry. !...
Calculate the net inductance of the following circuit. Assume each inductor to be 1 henry.
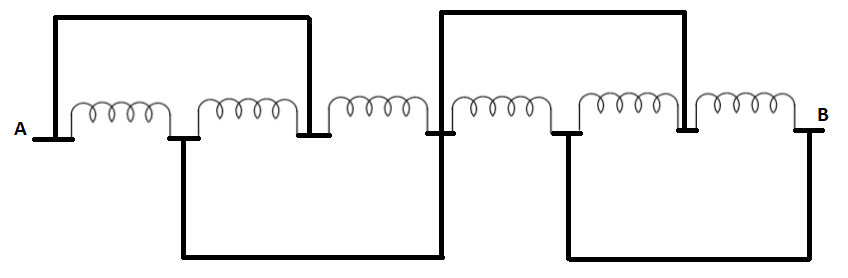
Solution
An inductor is a passive element used to temporarily store electrical energy in electronic circuits in the form of a magnetic flux or simply a magnetic field. The property of any coil that can set up the magnetic flux when the current passes through it is inductance. The SI unit of inductance is henry and it is denoted by H .
Formula Used: We know that when two inductors are connected in series combination, then the equivalent inductance, Leq=L1+L2
Also, when two inductors are connected in parallel combination, then the equivalent inductance, Leq=L1+L2L1L2 .
Complete solution Step-by-Step
According to the question, the inductance of each inductor shown in the circuit is equal to 1 henry.
Which means that L1=L2=L3=L4=L5=L6=H
The above circuit shown in the question can be broken down into a simpler form shown in the figure below
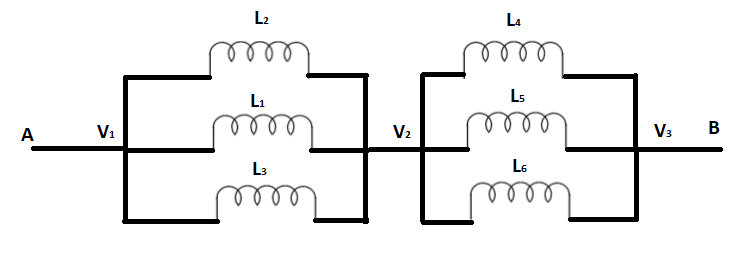
Thus, in part 1 of the figure:
L1 , L2 , and L3 are connected in parallel combination
So, the net equivalent of part 1 will be
Leq11=L11+L21+L31
Now we will put value of each inductance as 1H
⇒Leq11=H3
∴Leq1=3H
Similarly, in part 2 of the figure:
L4 , L5 , and L6 are connected in parallel combination
So, the net equivalent inductance of part 2 of the above circuit will be
Leq21=L41+L51+L61
∴Leq2=3H
Now we can observe that part 1 and part 2 are in series combination
So, the net equivalent inductance of the entire circuit will be
Leq=Leq1+Leq2
We will put the values of Leq1 and Leq2 in the formula above to get our final required answer
⇒Leq=3H+3H
∴Leq=32H .
Note
Inductance is a magnetic field that is proportional to the magnetic field's rate of change. For a conductor, this definition of induction holds. 1 henry is defined as the quantity of inductance required for a conductor to generate an emf of 1 volt when the current change in the conductor is 1A per second.
