Question

Calculate the moment of inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.

Answer 1

Hint: For calculating the moment of inertia of a regular shape with uniform mass density such as a semicircular disc, it is convenient to take a strip of infinitesimal mass, find out its moment of inertia as a function of some variable (such as the radial distance r) and then integrate it for the whole body.

Complete step by step answer:
Let the semicircular disc of mass M and radius R have a uniform mass density σ.
$\text{Mass density = }\dfrac{\text{Total mass of body}}{\text{cross sectional area}}$
Now, we know that the cross sectional area of a semicircular disk is $\dfrac{\pi {{R}^{2}}}{2}$ where R is the radius. The 2 factor comes in the denominator since the area of a semicircle is half of that of a circle.
Hence, mass density of the disc σ is
$\dfrac{\text{Total mass of body}}{\text{cross sectional area}}=\dfrac{M}{\dfrac{\pi {{R}^{2}}}{2}}=\dfrac{2M}{\pi {{R}^{2}}}$

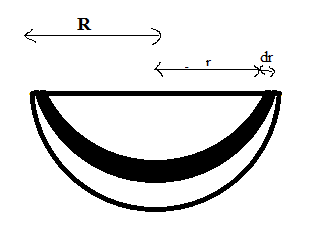
Now, we take an infinitesimally small semicircular strip of mass dm in the disc having the same thickness as that of the disc, width dr and at a distance r from the centre of the disc.
Therefore area of the strip =
$Perimeter\times width=\pi r\times dr$
Now, $\text{Mass of the strip }\left( \text{dm} \right)=\text{ mass density }\times \text{ area of strip}$
$=\dfrac{2M}{\pi {{R}^{2}}}\times \pi r\times dr=\dfrac{2Mr}{{{R}^{2}}}dr$
Moment of Inertia of the strip (dI) = $dm\times {{r}^{2}}=\dfrac{2Mr}{{{R}^{2}}}\times {{r}^{2}}dr=\dfrac{2M{{r}^{3}}}{{{R}^{2}}}dr$
Since, moment of inertia of a particle about a point =$\text{mass of particle}\times {{\left( \text{radial distance from point} \right)}^{2}}$
Now, integrating dI for the whole disc that is setting limits for r=0 to r=R, we get
$\int\limits_{0}^{I}{dI}=\int\limits_{r=0}^{r=R}{\dfrac{2M{{r}^{3}}}{{{R}^{2}}}}dr=\dfrac{2M}{{{R}^{2}}}\int\limits_{r=0}^{r=R}{{{r}^{3}}dr}=\dfrac{2M}{{{R}^{2}}}\times \dfrac{{{R}^{4}}}{4}=\dfrac{M{{R}^{2}}}{2}$
Therefore, the moment of inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane is $\dfrac{M{{R}^{2}}}{2}$.

Note: The moment of inertia of a semicircular disc about an axis passing through its centre and perpendicular to its plane could also have been found out intuitively if one knew the formula of moment of inertia for a full disk about the same axis which is $MR^2$. By general intuition, it is quite reasonable that since a semicircular disc is in essence half of the body of a full disc, its moment of inertia should also have been half of it.
Students may make mistakes in calculation as there is a bit of complex calculus involved. However, this is the most general approach to solving these types of questions where the moment of inertia of a uniform regular body is required. With a little practice, students will be able to quite easily derive other moment of inertia for other regular bodies also.
While finding out the moment of inertia in such problems, the axis about which the moment of inertia is asked should be understood carefully, since the moment of inertia of a body in general, changes about different axes.