Question

Calculate the mode.

Answer 1

To find the mode in this question, first of all we have to find the maximum frequency. So, to find the maximum frequency we have to use the equation of mean. That is, $mean=\dfrac{\sum{{{f}_{i}}{{x}_{i}}}}{N}$. By this we will get the mean of the class. Here, ${{x}_{i}}$ is mid-value of the class interval and ${{f}_{i}}$ is the frequency and N is the total frequency. After finding the mean of the class we can know the maximum frequency, that is the frequency of the modal class. Then, we have to find the mode using the equation $\bmod e=l+\dfrac{f-{{f}_{1}}}{2f-{{f}_{1}}-{{f}_{2}}}\times h$. Here, $l$= lower limit of modal class, $h$ = class width, $f=$ frequency of the modal class, ${{f}_{1}}=$ frequency of the class before modal class and ${{f}_{2}}=$ frequency of the class after modal class.

Complete step-by-step answer:
First of all we have to redraw the table that contains the mid-value and ${{f}_{i}}{{x}_{i}}$ columns. So, we will have a table as such,

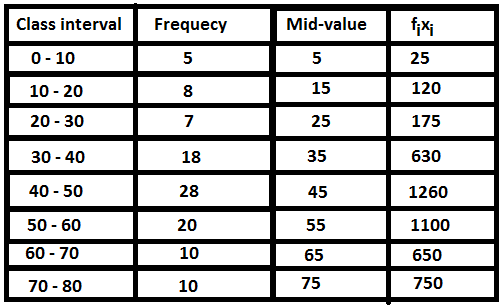
So, now we can find the modal class by using the equation,
$mean=\dfrac{\sum{{{f}_{i}}{{x}_{i}}}}{N}$
Here, ${{x}_{i}}$ is mid-value of the class interval and ${{f}_{i}}$ is the frequency and N is the total frequency.
$\sum{{{f}_{i}}{{x}_{i}}}=25+120+175+630+1260+1100+650+750=4440$
and $N=5+8+7+18+28+20+10+10=106$
So, $mean=\dfrac{\sum{{{f}_{i}}{{x}_{i}}}}{N}=\dfrac{4440}{106}=41.88$
So, the modal class is 40 – 50.
Therefore, the maximum frequency = 28.
Now, we have to find the mode of the class by using the equation,
$\bmod e=l+\dfrac{f-{{f}_{1}}}{2f-{{f}_{1}}-{{f}_{2}}}\times h$
Here, $l$ = lower limit of modal class, $h$ = class width, $f=$ frequency of the modal class, ${{f}_{1}}=$ frequency of the class before modal class and ${{f}_{2}}=$ frequency of the class after modal class.
So, we have
$l$ = 40
$h$ = 10
$f=$ 28
${{f}_{1}}=$ 18
${{f}_{2}}=$ 20
So, the equation becomes,
$\bmod e=40+\dfrac{28-18}{2(28)-18-20}\times 10$
$\bmod e=40+\dfrac{100}{18}$
On solving we get,
$\bmod e=45.55$
So, the mode is 45.55.

Note: We must be careful while taking the value of ${{f}_{1}}$ and ${{f}_{2}}$, sometimes we get confused while taking these values. Also be careful while finding $\sum{{{f}_{i}}{{x}_{i}}}$ because sometimes we might miss out 1 or 2 values.