Question
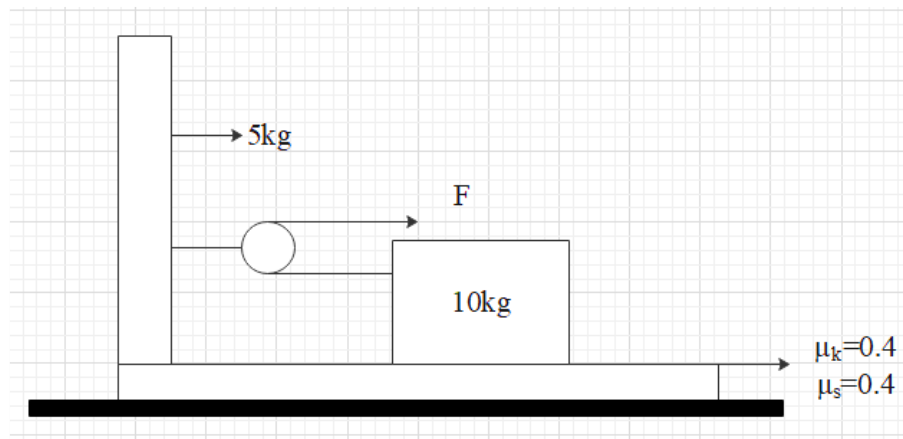
Question: Calculate the maximum force \(F\) that can be applied when the \(10Kg\) block is not to slide on the...
Calculate the maximum force F that can be applied when the 10Kg block is not to slide on the bracket?
A.32NB.24NC.18ND.48N
Solution
When the block does not slide on the bracket, we can check the block and bracket as one body, which has been experienced by the pulling force. The free-body diagram of the block shows that the tension on the rope must be identical everywhere along the rope. Find out the vertically and horizontally experienced forces. The acceleration of the body can be found by taking the ratio of the mass of the block to the whole mass of the system.
This all will help you in answering this question.
Complete step-by-step solution
When the block does not slide on the bracket, we can check the block and bracket as one body which has been experienced on by the pulling force,F
In order to get the force we can write that,
F=(m5+m10)a
The free body diagram of the block shows that the tension on the rope must be the identical everywhere along the rope,
∴T=F
Vertically the force can be shown to be as,
FN−mg=0⇒FN=m10g
In the horizontal direction, the balancing of the force has been taking place as the following,
Ff−T=m10a
From this we can say that,
Ff=μFN
The acceleration of the body can be found by taking the ratio of the mass of the block to the whole mass of the system.
a=m5+m10m10
Therefore the force can be written as,
F=m10a=F+m5+m10m10F
That is,
μ5m10g=F+m5+m10m10F⇒μ5m10g=F(1+m5+m10m10)
Rearranging this equation in terms of the force can be written as,
⇒F=μ5m10g(m5+2m10)(m5+m10)
Substituting the values in the equation can be shown as,
⇒F=0.4×10×9.8(25kg15kg)
Hence by simplifying this equation we can write that,
F=23.5N
The force has been calculated. The correct answer has been approximately given as option B.
Note: The acceleration of an object can be defined as the rate of variation of the velocity of the body with respect to the time taken. The velocity can be defined as the rate of variation of the displacement of the body with respect to the time taken. Both these quantities are found to be vectors.
