Solveeit Logo
Login

Question

Question: Calculate the magnitude of the magnetic field at a point \(100\text{ }cm\) from a long thin conducto...

Calculate the magnitude of the magnetic field at a point 100 cm100\text{ }cm from a long thin conductor carrying a current of 1 A1\text{ }A?

Explanation

Solution

We have to find the magnetic field for a point which is at a distance 100 cm100\text{ }cm from the long wire. It is given that the wire is long and straight, so it can be treated as a long infinite wire. By substituting the values of the variables in the equation to find the magnetic field due to a long infinite wire, we will find the answer.

Complete step by step answer:

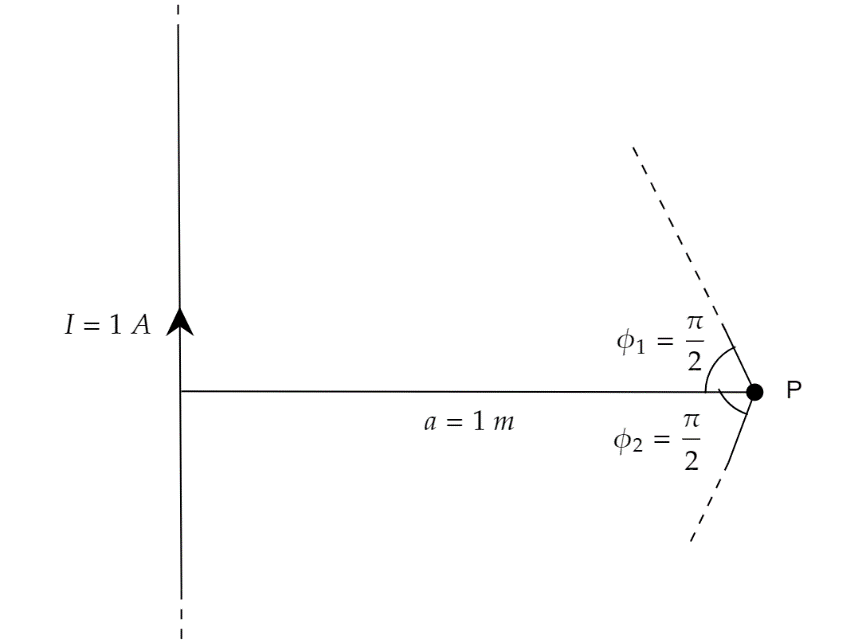
In the given question it is stated that we have to find the magnetic field of a point which is at a distance 100 cm100\text{ }cm from a long current carrying wire with a current of 1 A1\text{ }A.
According to Biot-Savart’s Law, the magnetic field at a point due to an wire is,
B=μ04πIa[sin⁡ϕ1+sin⁡ϕ2]−−(1)B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{I}{a}\left[ \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right]--\left( 1 \right)
The variables are defined as,
B=B= Magnetic field
I=I= current through the wire
a=a= distance between the point and the wire.
ϕ1{{\phi }_{1}} and ϕ2{{\phi }_{2}} are the angles that the point makes with both the ends.
It is said in the question that the wire is long and straight. Hence, we can consider it as an infinite wire.
In case of infinite wire we get, ϕ1=ϕ2=π2{{\phi }_{1}}={{\phi }_{2}}=\dfrac{\pi }{2}
Hence, [sin⁡ϕ1+sin⁡ϕ2]=sin⁡π2+sin⁡π2=1+1=2\left[ \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right]=\sin \dfrac{\pi }{2}+\sin \dfrac{\pi }{2}=1+1=2
Substituting the value in equation (1)\left( 1 \right) we get, the magnetic field due to a long infinite wire is,
B=μ02πIa−−(2)B=\dfrac{{{\mu }_{0}}}{2\pi }\dfrac{I}{a}--\left( 2 \right)
Hence
The value of μ02π=2×10−7\dfrac{{{\mu }_{0}}}{2\pi }=2\times {{10}^{-7}}
Given,
I=I= current through the wire=1 A=1\text{ }A
a=a= the distance between the point and the wire=100 cm=1 m=100\text{ }cm=1\text{ }m
Substituting the values in the equation (2)\left( 2 \right) we get,
B=2×10−7×11=2×10−7B=2\times {{10}^{-7}}\times \dfrac{1}{1}=2\times {{10}^{-7}}
The magnetic field at a point which is at a distance 100 cm100\text{ }cm from a long thin conductor carrying a current of 1 A1\text{ }A is 2×10−7 T2\times {{10}^{-7}}\text{ }T.

Note:
It must be noted that in case of Biot-Savart’s Law due to an infinite wire, the point makes angle approximately, 90∘{{90}^{\circ }} with both the ends of the wire as the wire is infinite. The original formula for the Biot-Savart’s Law is B=μ02πIa[sin⁡ϕ1+sin⁡ϕ2]B=\dfrac{{{\mu }_{0}}}{2\pi }\dfrac{I}{a}\left[ \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right].