Question

Calculate the lattice energy of a salt $MX(s)$​ from the date given below:
Heat of formation of $MX\left( {\Delta H} \right)\; = - 550\;kJ/mol$
Heat of sublimation of $M\left( S \right) = 80\;kJ/mol$
Heat of dissociation of ${X_2}\left( D \right) = 155\;kJ/mol$
Ionization energy of $M\left( {IE} \right) = 347\;kJ/mol$
Electron affinity of $X\left( {EA} \right) = - 343\;kJ/mol$
A. $- 835KJ/mol$
B. $- 938.5{\text{ }}kJ/mol$
C. $- 711.5{\text{ }}kJ/mol$
D. $- 638.5{\text{ }}kJ/mol$

Answer 1

Born Haber cycle is mainly used to calculate the lattice energy. It also involves steps such as sublimation energy $\left( {\Delta {H_{sub}}\;} \right),$ dissociation energy $\left( D \right),$ ionisation energy$\left( I \right),$ electron affinity$\left( E \right)$ and heat of formation of crystal $\left( H \right).$ Represented in the form of
$\Delta {\text{ }}H{\;_{f{\;^0}}}\; = {\text{ }}\Delta H\;sub\; + {\text{ }}\dfrac{D}{2} + {\text{ }}IE{\text{ }} + {\text{ }}EA\; + U$

Complete step by step answer:
Born Haber cycle is a cycle of enthalpy change of process and The energy terms involved in building a crystal lattice$\left( {{\text{ }}MX} \right)$ such as -
Step$\;1$ - convert solid $\left( {{\text{ }}M} \right)$ to gaseous $\left( {{\text{ }}M} \right)$is called enthalpy of sublimation $\left( {\Delta H\;sub} \right).$
Step $2$ - convert gaseous$\left( X \right)$ molecule to atoms is called enthalpy of dissociation$\left( D \right).$
Step $3$ - Conversion of gaseous $\left( {{\text{ }}M} \right)$ atom into $\left( {M{\text{ }}ion} \right)$ in gaseous state is called ionisation energy .
Step $4$ - Conversion of gaseous $\left( X \right)$ atom into gaseous $X{\text{ }}\;ion$ is known as electron gain enthalpy and represented by ${E_A}\;.$
Step $5$ - The amount of energy released when one mole of solid crystalline compound is obtained from gaseous ions is called lattice energy$\left( U \right)$
$M\left( s \right) + {\text{ }}\dfrac{1}{2}X\;\left( g \right) \to MX\left( s \right)$
The Born-Haber Cycle can be reduced to a single equation:
Heat of formation= Heat of atomization + Dissociation energy+ (sum of Ionization energies) + (sum of Electron affinities)+ Lattice energy

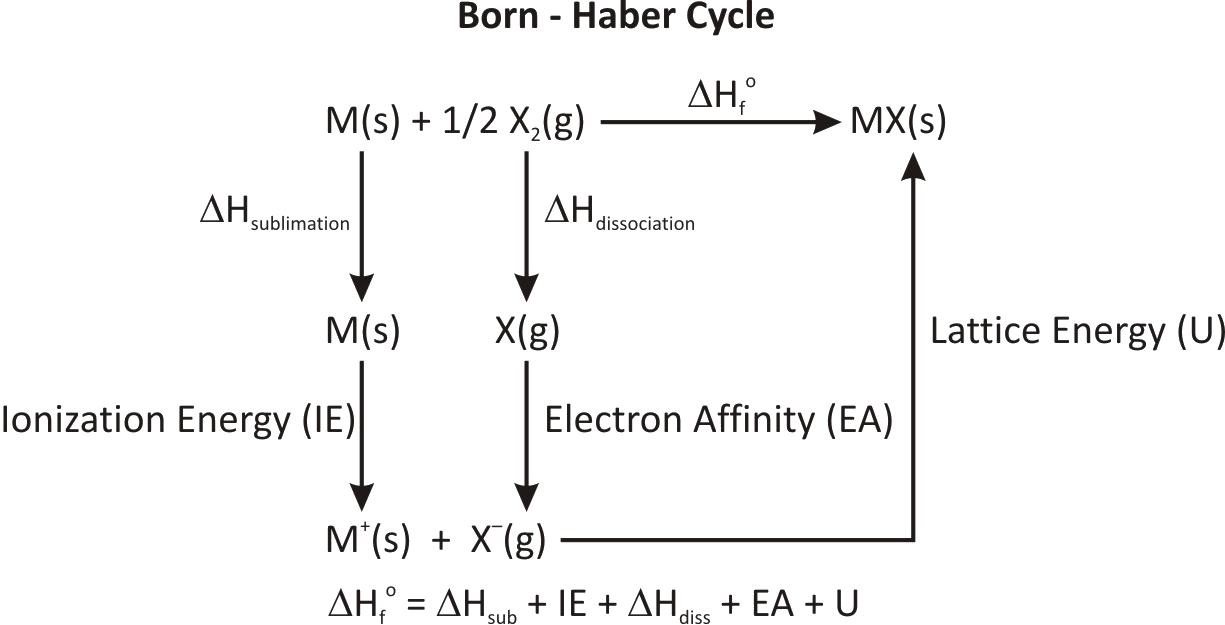
The enthalpies are represented in figure.
These steps are represented as -
$\Delta {\text{ }}H{\;_f}^0\; = {\text{ }}\Delta H{\;_{sub}}\; + {\text{ }}D/2{\text{ }} + {\text{ }}IE{\text{ }} + {\text{ }}{E_A}\; + U$
Now, Putting values as -
$\Delta {H_f}\; = \;\;\;S{\text{ }} + {\text{ }}0.5D{\text{ }} + {\text{ }}IE{\text{ }} + {\text{ }}EA{\text{ }} + {\text{ }}U$
$- 550{\text{ }} = \;\;80 + \dfrac{{155}}{2} + 347 - 343 + U$
$\;\;U = - 711.5kJ/mol$
lattice energy of salt $= \; - 711.5\;kJ/mol.$
Option (c ) is correct.
Note: Born Haber process is a method that allows us to observe and analyze energies in a reaction. It mainly helps in describing the formation of ionic compounds from different elements. Born Haber cycle is a process that leads to the formation of a solid crystalline ionic compound from the elemental atoms in their standard state and of the enthalpy of formation of the solid compound such that the net enthalpy becomes zero.