Question

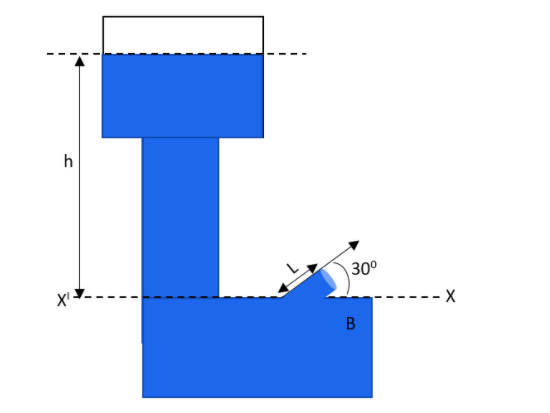
Calculate the height above the dashed line $X{X}'$ attained by the water stream coming out through the hole which is placed at point B in the figure given. Given that $h=10m,L=2m\text{ and }d=30{}^\circ$.

$\begin{aligned} & A.10m \\\ & B.7.1m \\\ & C.5m \\\ & D.3.2m \\\ \end{aligned}$

Answer 1

First of all analyse the diagram given. Torricelli's theorem is the basis for solving this question. The velocity of the jet is found by taking the square root of the twice of the product of the acceleration due to gravity and difference between the heights. This will help you in solving this question.

Complete step by step answer:
It has been given that,
Height has been given as,
$H=10m$
Length has been mentioned as,
$L=2m$
And the angle can be shown as,
$\theta =30{}^\circ$
From the figure we can find that,
$h=2\times \sin \theta$
Substituting the values in the equation will give,
$\begin{aligned} & h=2\times \sin 30{}^\circ \\\ & \Rightarrow h=1m \\\ \end{aligned}$
According to Torricelli's theorem, the velocity of the jet is found by taking the square root of the twice of the product of the acceleration due to gravity and difference between the heights. That is we can write that,
$v=\sqrt{2g\left( H-h \right)}$
Substituting the values in it,
$\begin{aligned} & v=\sqrt{2\times 9.8\left( 10-1 \right)} \\\ & \Rightarrow v=13.3m{{s}^{-1}} \\\ \end{aligned}$
The height of the jet from the opening of orifice at the lower end can be written as,
${H}'=\dfrac{{{v}^{2}}{{\sin }^{2}}30{}^\circ }{2g}$
Substituting the values in it will give,
${H}'=\dfrac{{{13.3}^{2}}\times \dfrac{1}{4}}{2\times 9.8}=2.2m$
Height from the line $X{X}'$ will be found as,
$H={H}'+h$
Substituting the values in it will give,
$H=2.2+1=3.2$
Hence the maximum height of the jet can be written as $3.2m$. The answer has been given as option D.

Note: Torricelli's law is otherwise called Torricelli's theorem. This theorem is helpful in fluid dynamics which is connected with the speed of fluid flowing from an orifice to the height of fluid above the opening. This law is having a lot of physical daily applications also.