Question
Question: Calculate the force F required to cause the block of weight \({{W}_{1}}=200N\) just to slide under t...
Calculate the force F required to cause the block of weight W1=200N just to slide under the block of weight W2=100N. What is the tension in the string AB? [Coefficient of friction μ=0.25 for all surfaces in constant].
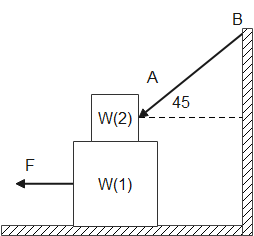
Solution
In this question we will also be using newton’s third law of motion which is also known as action reaction, this law states that every action has an equal and opposite reaction. This law deals with the direction too. Since it states that there will be equal and also opposite reactions. Opposite means that the direction will be opposite.
Complete answer:
In the question we have been given with two blocks and coefficient of friction, The given quantities are as follows
Weight of block 1 is W1=200N
Weight of Block 2 is W2=100N
Coefficient of friction μ=0.25
Additionally, we have given an angle which is equal to 45∘
Now we know that the force of friction can be given as
Ff=μN
Where Ffis the frictional force and N is the normal force or normal reaction.
μ is the coefficient of friction
Now Normal reaction will be equal to the weight of the object as there is no other force acting in downward or upward direction
So, N1=W1 and N2=W2
But as shown in the above figure the frictional force on the lower block or 1st block will be due to the weight of both the blocks. So,
F1=μ(W1+W2)
Where F1 is the frictional force due on block 1 or on lower block
While in case of upper or 2nd block the force will be only due to weight of 2nd block
F2=μW2
Where F2 is the frictional force due to the 2nd block.
Now the total force will be
F=F1+F2
F=μ(W1+W2)+μW2
Now putting the values in above equation, we get
F=0.25(200+100)+0.25(100)
F=100N
Hence 100 N of force is required to slide the block
Now in the question we have been asked about the tension in the string
So, by using newton's third law we get,
F=−T
Therefore (-100N) of tension will be there in the string
Note:
In the answer, we have negative signs. Negative sign in the value of tension denotes the direction, it does not mean that the force will be negative. The negative sign indicates that the tension will act in the opposite direction as that of force. Which is absolutely correct and satisfies newton’s third law of motion
