Question

Calculate the equivalent resistance from point A to B?

Answer 1

First to solve the problem O is the junction to all the current so we can write it O, O’ and O’’. In every step draw the total resistance in each of the branches. Here we have to solve this problem by using both parallel and series resistance formulas. Finally adding and simplifying step by step we can find the equivalent resistance of the given diagram.

Complete step by step answer:
We need to calculate the equivalent resistance across the A and B as per the given figure:

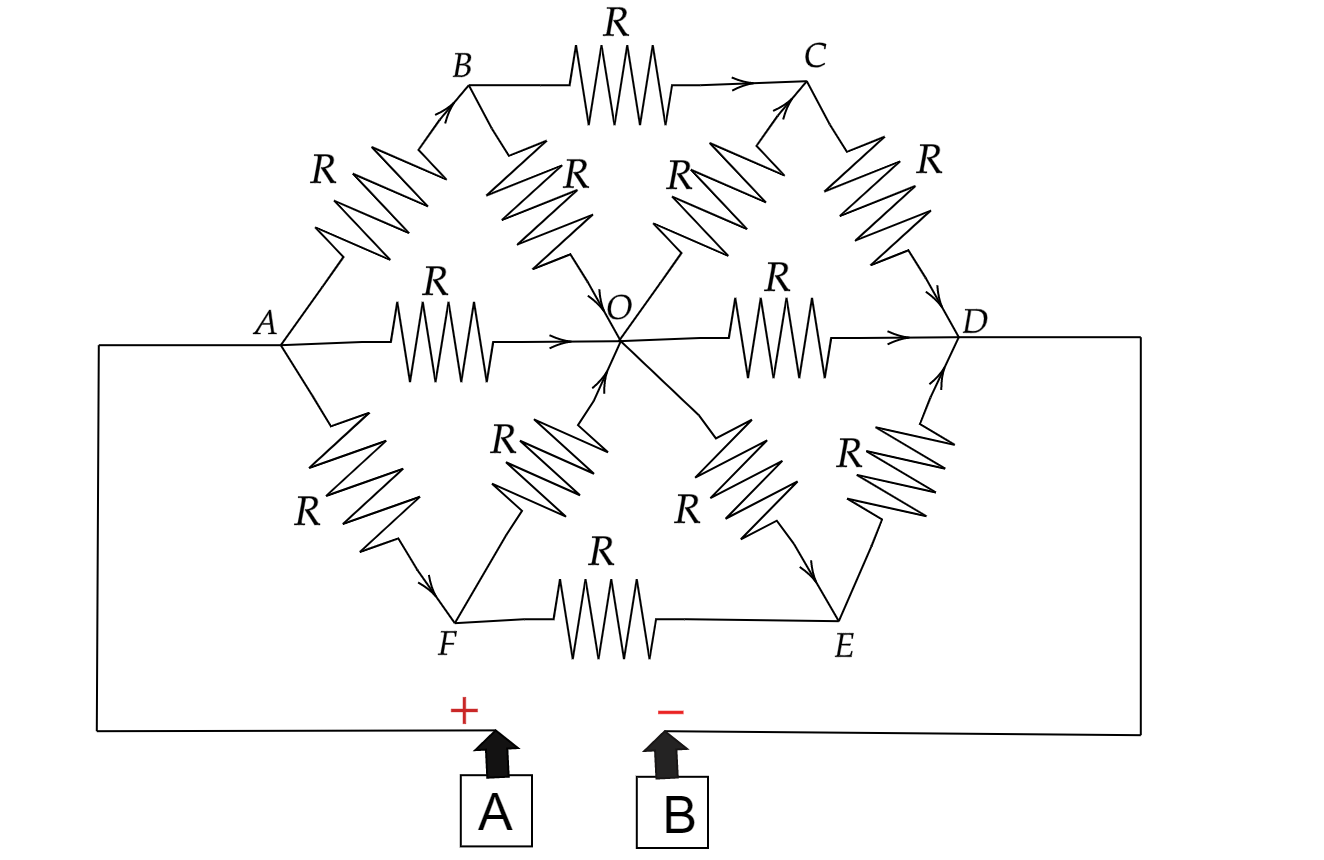
From the figure we can see that point O is the junction of all branch currents. Now represent the point O in three different points as O, O’ and O’’. Hence we will get,

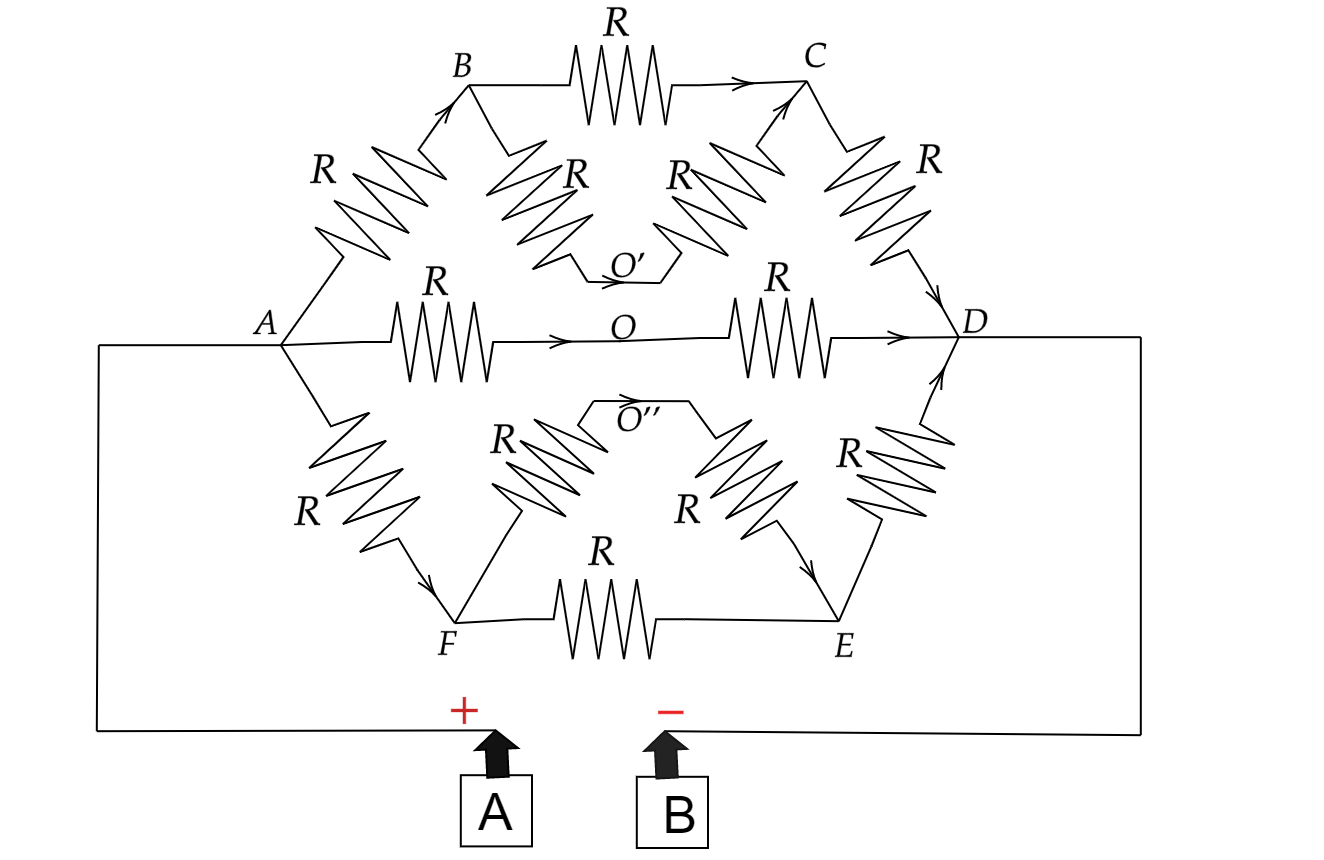
Now we have to solve this circuit branch by branch in each step at the same time to draw the total resistance in that branch.
Total Resistance in BO’C branch we will get,
Both the resistance in this branch are in series with each other hence we will get,
${R_{BO'C}} = {R_{BO'}} + {R_{O'C}}$
From figure we will get,
$\Rightarrow {R_{BO'C}} = R + R = 2R$
Similarly total resistance in FO’’E branch we will get,
Both the resistance in this branch are in series with each other hence we will get,
${R_{FO''E}} = {R_{FO''}} + {R_{O''E}}$
From figure we will get,
$\Rightarrow {R_{FO''E}} = R + R = 2R$
In branch AD the two resistance are in series hence the total resistance in that branch is,
${R_{AD}} = R + R = 2R$
Now the figure will look like:

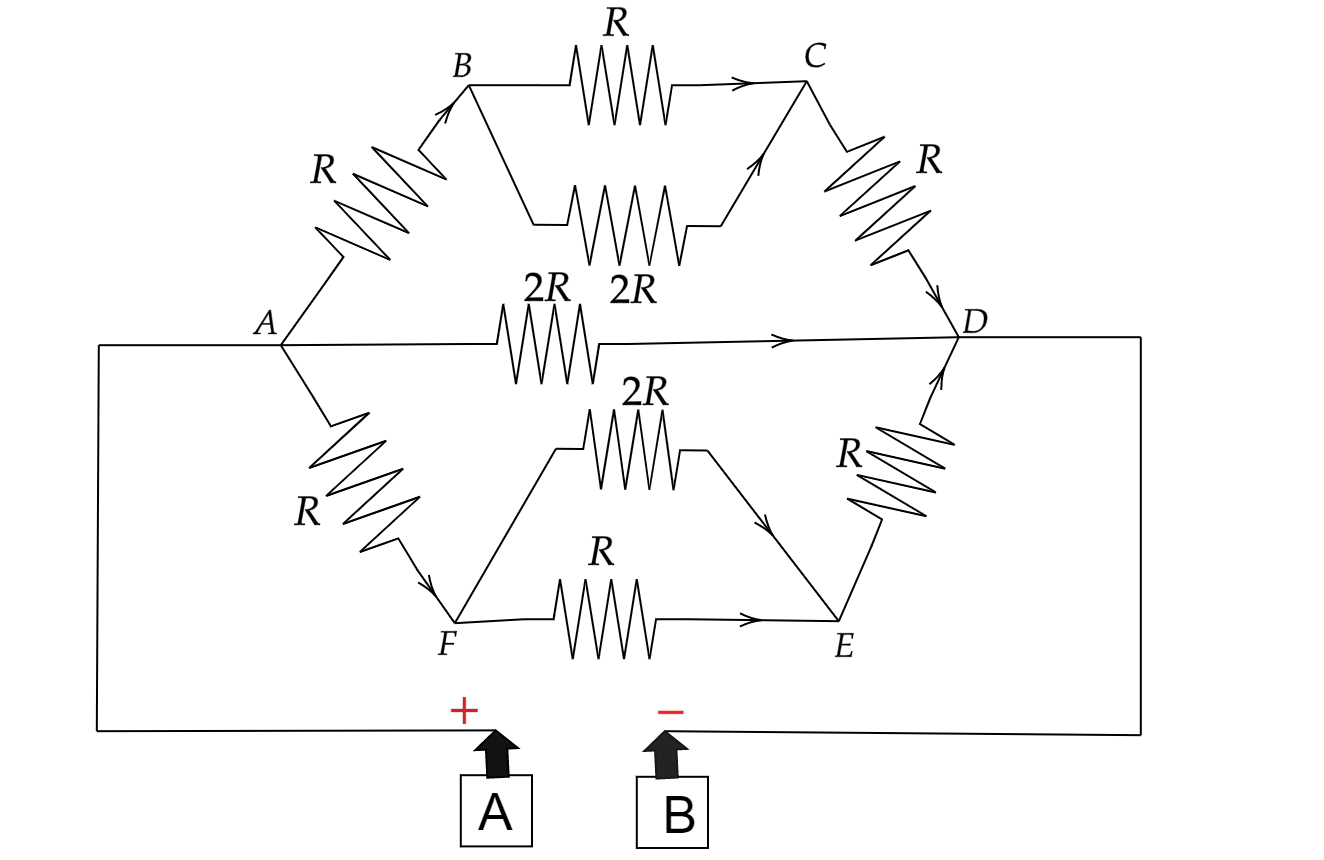
Now in branch BC the two resistance are parallel to each other so we will get,
${R_{BC}} = R||2R$
Hence,
${R_{BC}} = \dfrac{{R \times 2R}}{{R + 2R}} = \dfrac{{2R}}{3}$
Similar in branch FE the two resistance are parallel to each other so we will get,
${R_{FE}} = R||2R$
Hence,
${R_{FE}} = \dfrac{{R \times 2R}}{{R + 2R}} = \dfrac{{2R}}{3}$
Now the figure will look like,

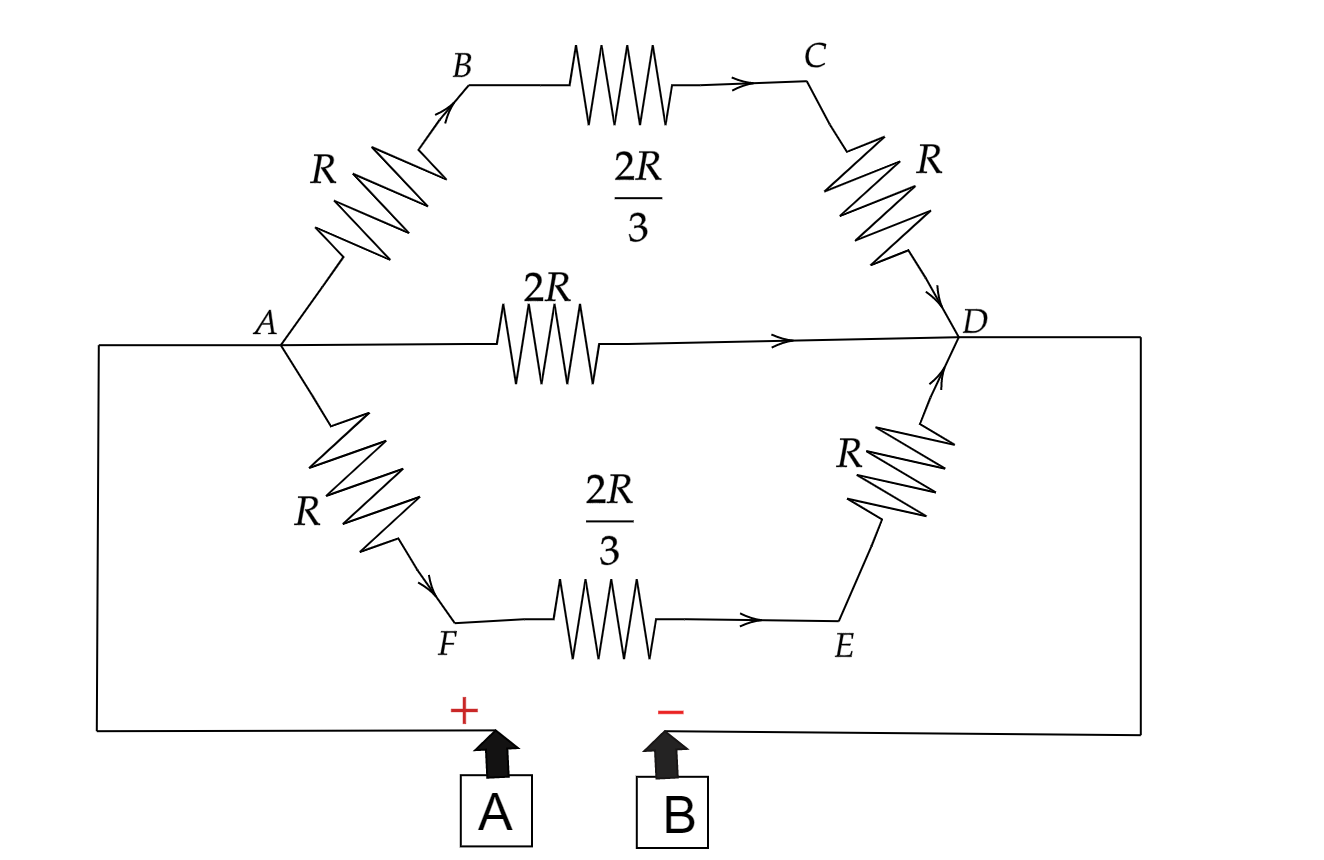
The total resistance in upper part of AD is given as,
${R_{UAD}} = R + \dfrac{{2R}}{3} + R = \dfrac{{8R}}{3}$
Similarly the total resistance in lower part of AD is given as,
${R_{LAD}} = R + \dfrac{{2R}}{3} + R = \dfrac{{8R}}{3}$
Now the figure will look like,

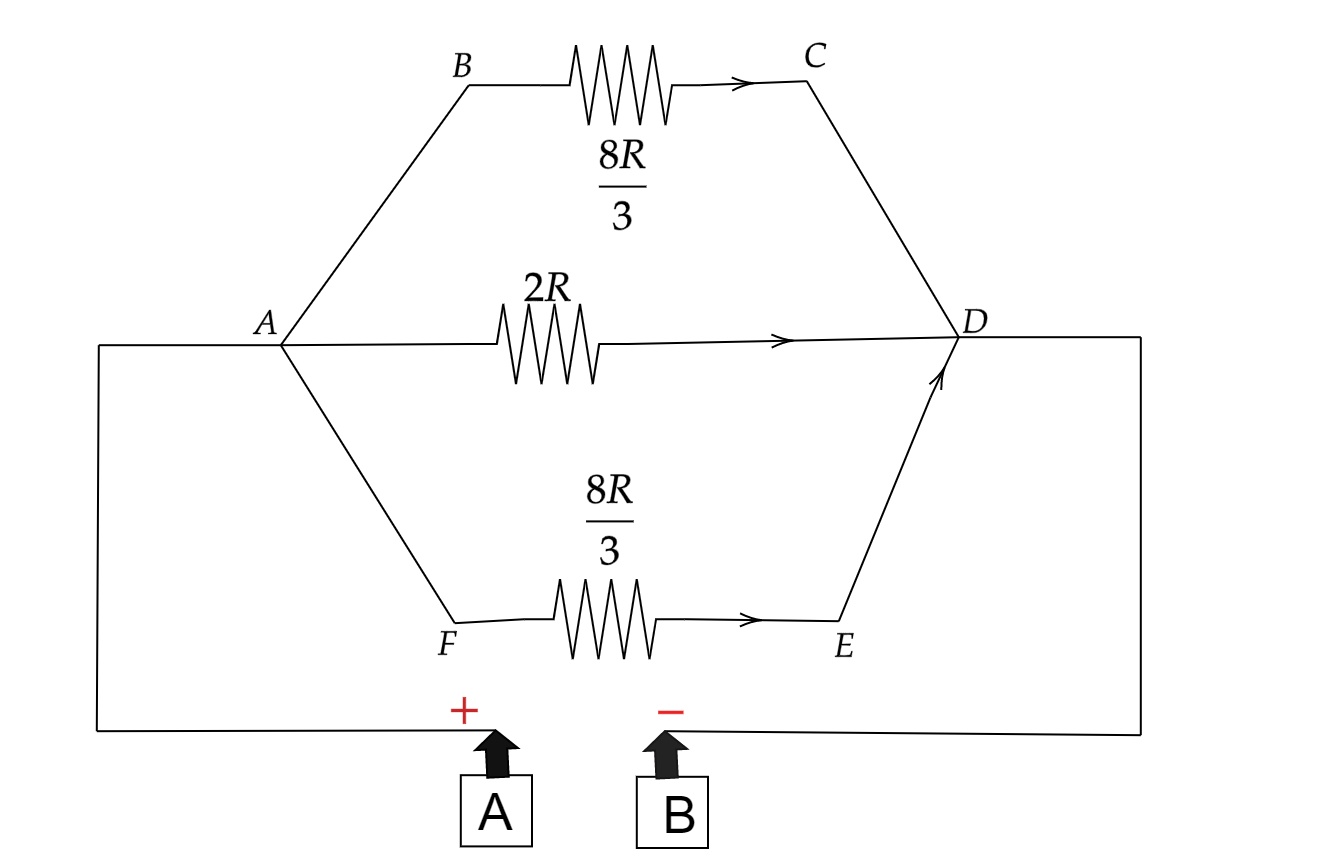
Now we can calculate the equivalent resistance across the point A and B.
The three resistance are parallel to each other hence the equivalent resistance will be,
$\dfrac{1}{{{R_{{\text{eq}}}}}} = \dfrac{1}{{\dfrac{{8R}}{3}}} + \dfrac{1}{{2R}} + \dfrac{1}{{\dfrac{{8R}}{3}}}$
$\Rightarrow \dfrac{1}{{{R_{{\text{eq}}}}}} = \dfrac{3}{{8R}} + \dfrac{1}{{2R}} + \dfrac{3}{{8R}} = \dfrac{{3 + 4 + 4}}{{8R}} = \dfrac{{10}}{{8R}}$
Now rearranging the above equation we will get,
${R_{{\text{eq}}}} = \dfrac{{8R}}{{10}} = 0.8R\Omega$

Note: After solving each branch resistance you must draw the circuit. Remember that the equivalent resistance is where the total resistance is connected either in parallel or in series. The electrical resistance shows how much energy will be required when we move the charges that are the current through the circuit.