Question
Question: Calculate the equivalent resistance between the points A and B for the following combination of resi...
Calculate the equivalent resistance between the points A and B for the following combination of resistors:
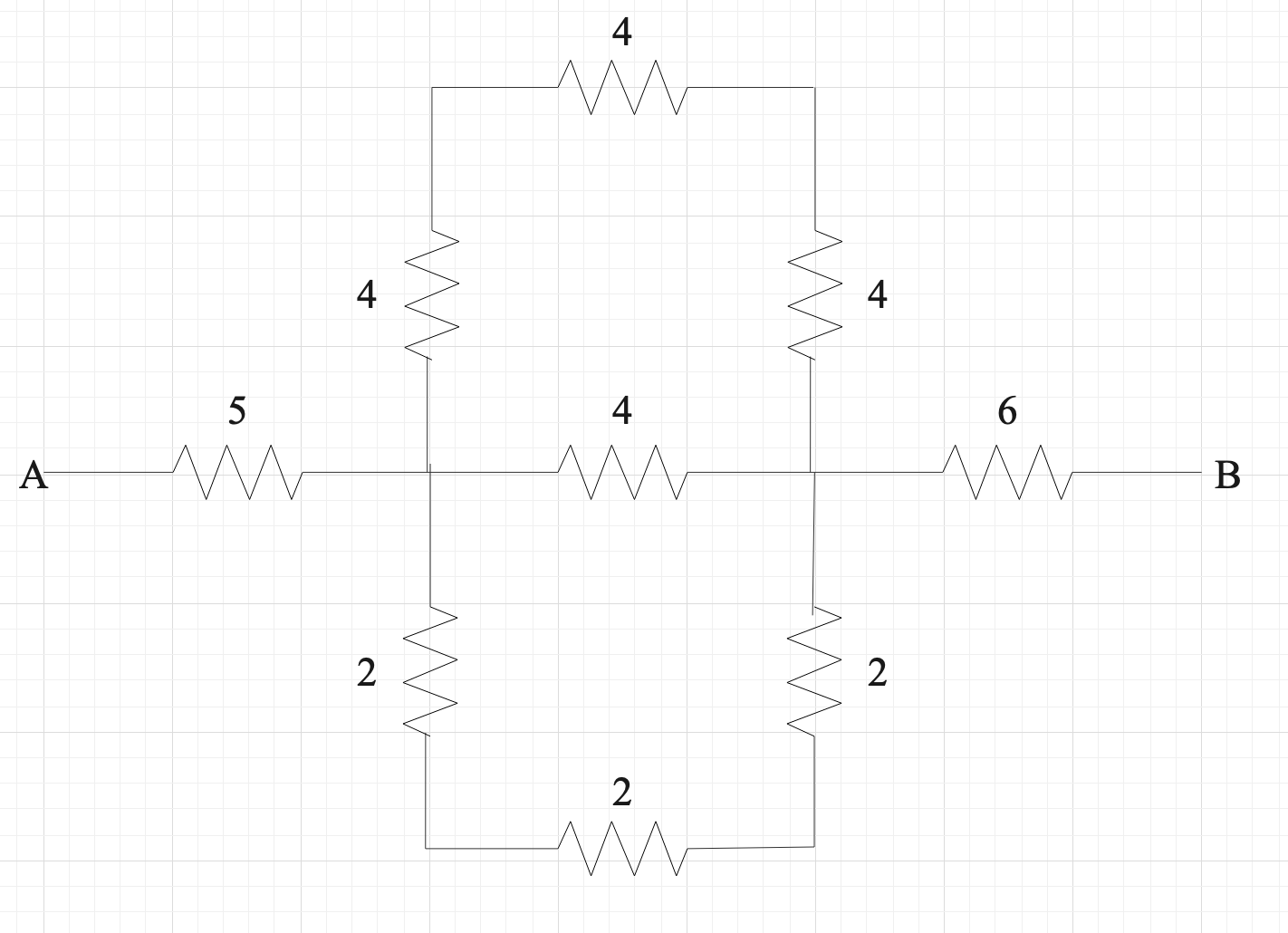
Solution
Hint: First find the series connections, then solve the parallel connection. Divide the circuit into three segments. Find the equivalent resistance for the middle segment using parallel and series connection formulas. Then calculate the final equivalent resistance using the simple series formula.
Formula Used:
The equivalent resistance of 3 parallel resistors is given by,
R=R1R2+R2R3+R3R1R1R2R3.....................(1)
The equivalent resistance of 3 series resistors is given by,
R=R1+R2+R3.....................(2)
Where,
R1 is the resistance of the first resistor,
R2 is the resistance of the second resistor,
R3 is the resistance of the third resistor.
Complete step by step answer:
First, let us look at the circuit diagram,
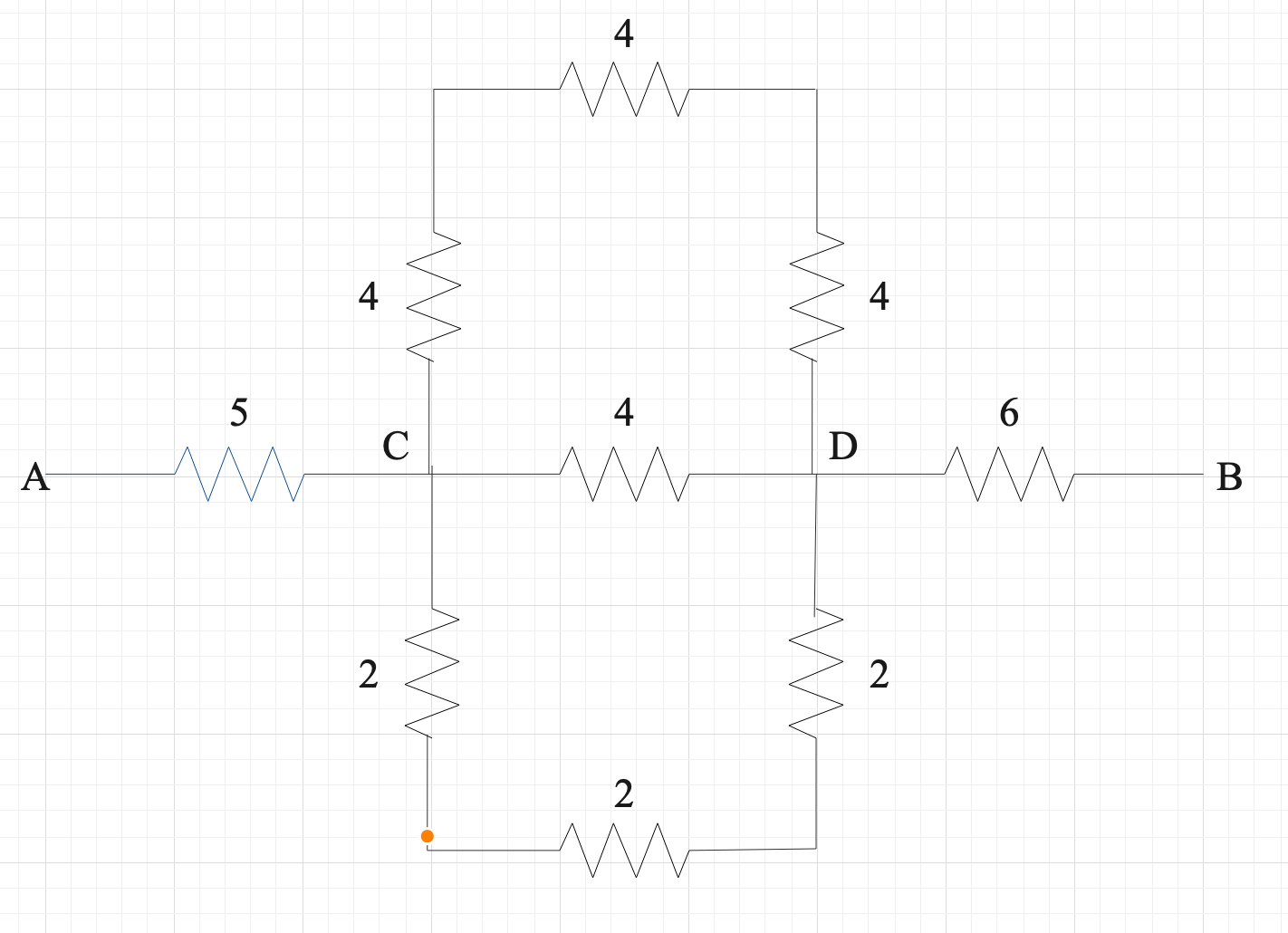
For simplicity, we can divide the circuit diagram into three segments,
AC, CD, and DB.
First, let us solve the CD segment.
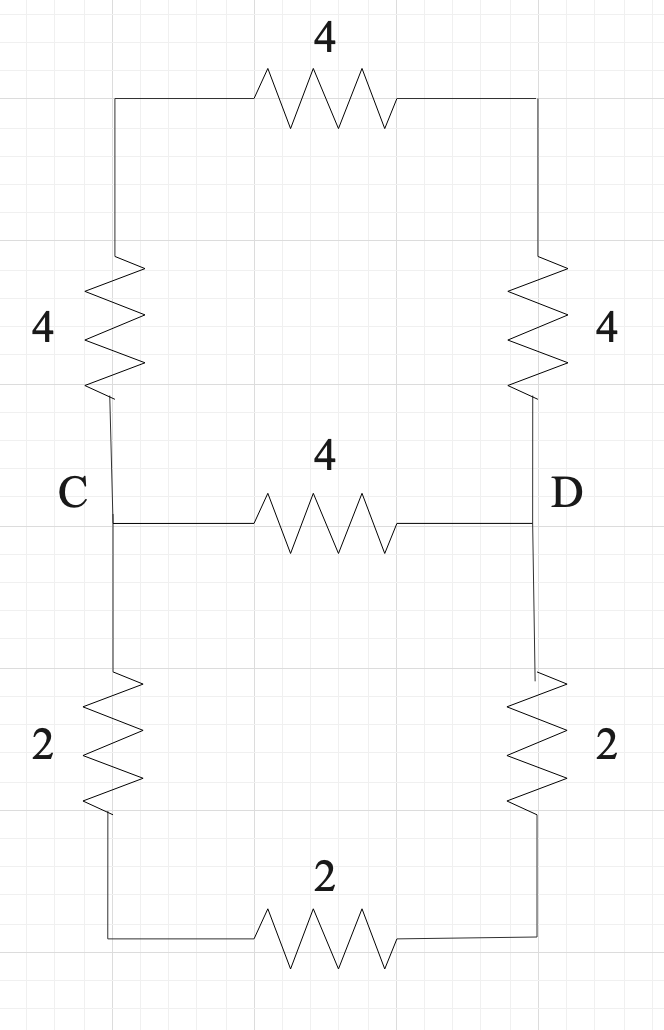
So, the 4Ω resistances are connected in series, so the equivalent resistance of the top branch is -
(4+4+4) Ω = 12Ω
Now, the equivalent resistance of the bottom branch is -
(2+2+2) Ω = 6Ω
So, the CD segment should look like this:
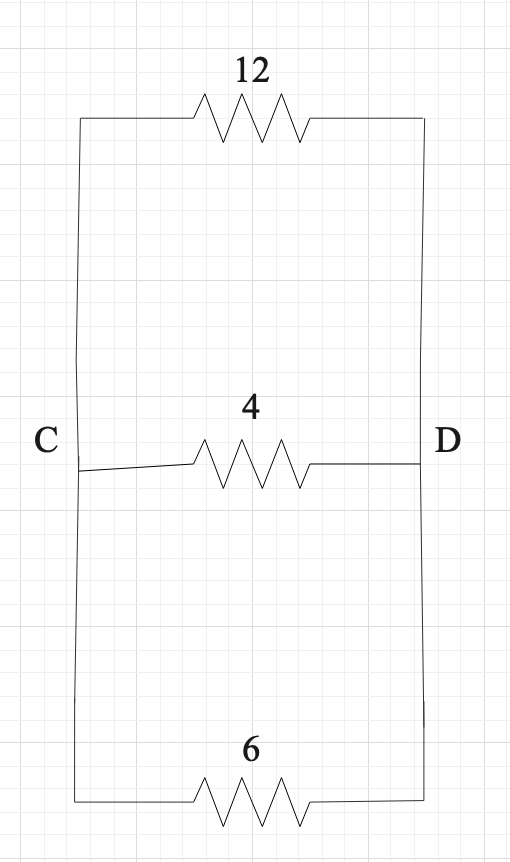
Now we use equation (1) to get the equivalent resistance of the resistance system.
The equivalent resistance of the CD segment is,
RCD=R1R2+R2R3+R3R1R1R2R3
⇒RCD=12×4+4×6+6×1212×4×6=2
Hence the overall circuit diagram should like this,
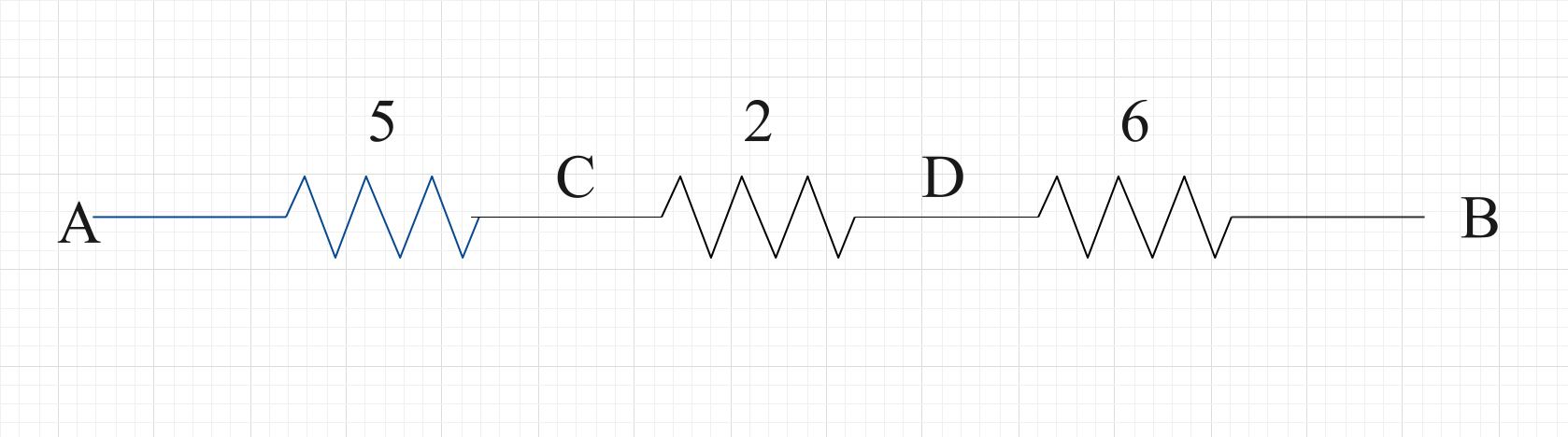
This is a simple series connection. So, the equivalent resistance of the system is,
RAB=(5+2+6)=13
The equivalent resistance between points A and B = 13 Ω
Note: We have used a complex formula for the parallel system. You can use the simple formula shown below to calculate the equivalent resistance of the system.
R1=R11+R21+R31.....................(3)
Where,
R1 is the resistance of the first resistor,
R2 is the resistance of the second resistor,
R3 is the resistance of the third resistor.
You can use equation (3) to calculate the equivalent resistance of the parallel system. The calculation will be less in some cases.
