Question
Question: Calculate the equivalent resistance between a and b of the following network of conductors. 
A. 4Ω
B. 5Ω
C. 3Ω
D. 2Ω
Solution
We can clearly see that the given circuit is the Wheatstone bridge circuit. We will first determine whether this circuit is balanced or unbalanced. After then, we will calculate the equivalent resistance based on the type of the bridge, balanced or unbalanced.
Complete step by step answer:
Let us first determine whether the given circuit is balanced or unbalanced.The ratio of the resistances on the left hand arms is 25 and the ratio of the resistances on the right arms is 42=21. As these both are not equal, the given Wheatstone bridge is unbalanced.
Now, we will find the equivalent resistance of this network step by step.Our first step is to convert the delta network to star network.As shown in figure, three resistances of 5Ω, 2Ω and 3Ω forms delta connection. So, we will convert this delta connection into a star connection of three resistances PΩ, QΩ and RΩ as shown in the figure.
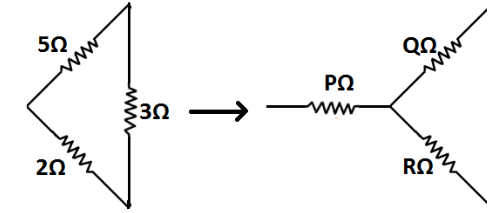
Now, we will find the resistances PΩ, QΩ and RΩ by using the rules of conversion from delta to star conversion.
⇒P=5+2+35×2=1010=1Ω
⇒Q=5+2+35×3=1015=1.5Ω
⇒R=5+2+32×3=106=0.6Ω
Thus, our main circuit will become as shown in the following figure.
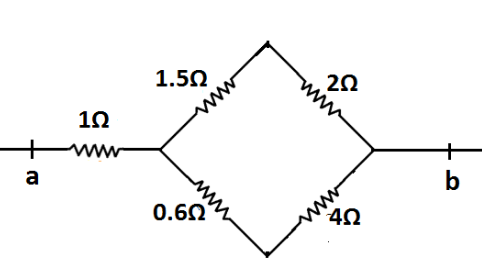
From the figure it is clear that resistances 1.5Ω and 2Ω are in series connection.We know that the equivalent resistance of two resistances connected in series is given by Req=R1+R2
Therefore, the equivalent resistance of 1.5Ω and 2Ω is 1.5+2=3.5Ω
Similarly, the equivalent resistance of 0.6Ω and 4Ω is 0.6+4=4.6Ω
Thus, our main circuit will become as shown in the following figure.
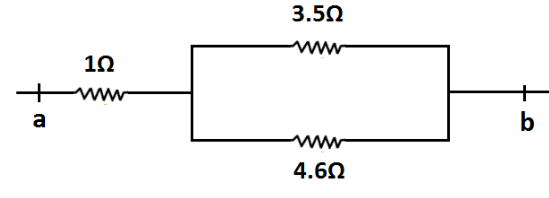
From the figure it is clear that resistances 3.5Ω and 4.6Ω are in parallel connection.We know that the equivalent resistance of two resistances connected in parallel is given by Req=R1+R2R1R2
Therefore, the equivalent resistance of 3.5Ω and 4.6Ω is 3.5+4.63.5×4.6=1.99Ω
Now, our main circuit will become as shown in the following figure.Here, resistances 1Ω and 1.99Ω are in series connection.Therefore, the equivalent resistance of 1Ω and 1.99Ω is 1+1.99=2.99≈3Ω
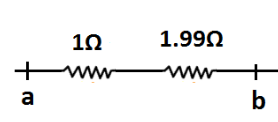
Here, resistances 1Ω and 1.99Ω are in series connection.Therefore, the equivalent resistance of 1Ω and 1.99Ω is 1+1.99=2.99≈3Ω.
Finally, our circuit will be as shown in the following figure.
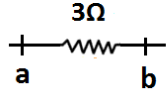
Thus, the equivalent resistance between a and b of the given network of conductors is 3Ω .
Hence, option C is the right answer.
Note: In this type of question where the Wheatstone circuit is given, it is important to know if it is balanced or unbalanced. Here, the given circuit is unbalanced, therefore we have first converted the delta connection to star connection. And then, we have applied the laws of equivalent resistance for series and parallel connections to get our final answer.
