Question

Calculate the equivalent capacitance across A and B.

$\begin{aligned} & A.\dfrac{35}{6}\mu F \\\ & B.\dfrac{25}{6}\mu F \\\ & C.15\mu F \\\ & D.\text{none of these} \\\ \end{aligned}$

Answer 1

The circuit can be converted to a wheatstone bridge which can be helpful in solving the question. As we all know, the capacitors which are connected in parallel will be having an equivalent capacitance as the sum of the individual capacitance. When they are connected in series the reciprocal of resultant capacitance will be taken as the sum of the reciprocal of the individual capacitances. These all may help you to solve this question.

Complete step by step answer:
This circuit can be redrawn by taking some kind of equivalent capacitance.
When we look into the capacitors $15\mu F$ and $10\mu F$ which are connected at the A terminal, we can see that they are connected in parallel. Therefore their resultant can be taken as,
${{C}_{eq}}=10+15=25\mu F$
And also when we look at terminal B, we can see that the both the capacitors of capacitance $1\mu F$are connected in parallel. Therefore their equivalent resistance will be given as,
${{C}_{eq}}=1+1=2\mu F$
These equivalent capacitance can be shown in the diagram by redrawing it. That is,

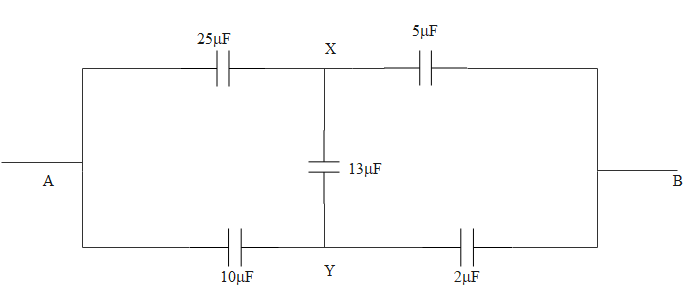
From the figure we can see that now the circuit has been transformed into a wheatstone bridge. As it is a wheatstone bridge, the potential at the X and Y are similar. Therefore we can write that,
${{V}_{X}}={{V}_{Y}}$
Hence we can say that,
$\dfrac{25\mu F}{5\mu F}=\dfrac{10\mu F}{2\mu F}$
Now we can see that the capacitors, $5\mu F$ and $25\mu F$are in series. In the same way, $10\mu F$ and $2\mu F$are in series. The resultant of both of these will be parallel. Therefore we can write that,
${{{C}'}_{eq}}=\left( \dfrac{5\times 25}{5+25} \right)+\left( \dfrac{10\times 2}{10+2} \right)=\dfrac{35}{6}\mu F$
Therefore the correct answer has been obtained. It is given as option A.

Note:
Capacitance is defined as the ratio of the electric charge on each conductor to the potential difference or the voltage between them. The capacitance value of a capacitor is generally taken in farads. A capacitor is used to store electrical energy in metallic plates.