Question

Calculate the effective capacitance between points M and N.

A. $10\mu F$
B. $5\mu F$
C. $15\mu F$
D. $7\mu F$

Answer 1

To solve this question, we need to understand the concept of the parallel and series connection of the capacitors. Also, we need to check whether any capacitor is short circuited. This is because we do not have to consider the capacitor which is short circuited while calculating the effective capacitance.

Formulas used:
When two capacitors are connected in parallel connection, their equivalent capacitance is given by:
${C_{eq}} = {C_1} + {C_2}$
When two capacitors are connected in series connection, their equivalent capacitance is given by:
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$

Complete step by step answer:
Let us solve the given circuit step by step. First we can see that two capacitors of $6\mu F$at the starting point near M are connected in parallel connection. Therefore their equivalent capacitance can be determined by the formula ${C_{eq}} = {C_1} + {C_2}$.Now, our circuit becomes as:

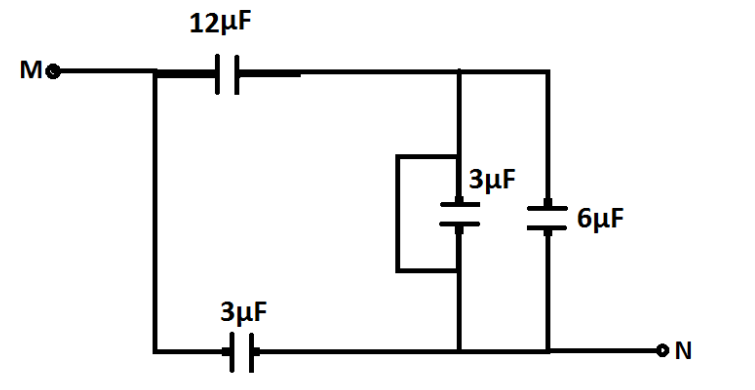
Now, we can see that the capacitor on the right side having $3\mu F$ is short circuited.Therefore, it becomes zero. Thus, our circuit becomes:

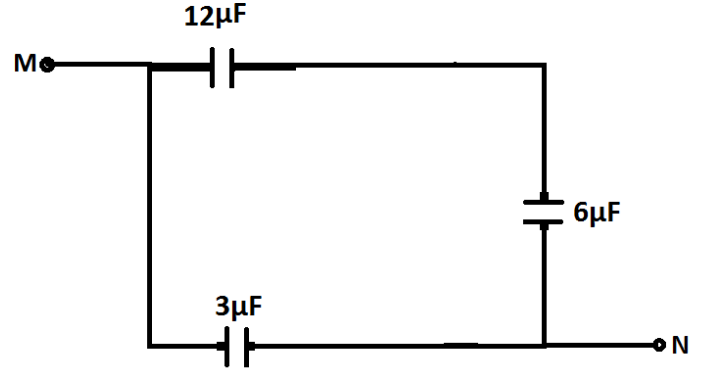
Now, we can see that the capacitors of $12\mu F$and $6\mu F$are connected in series.Therefore their equivalent capacitance can be determined by the formula $\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$ as
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{12}} + \dfrac{1}{6} = \dfrac{3}{{12}} = \dfrac{1}{4} \\\ \Rightarrow {C_{eq}} = 4\mu F \\\$
Now, our circuit becomes as:

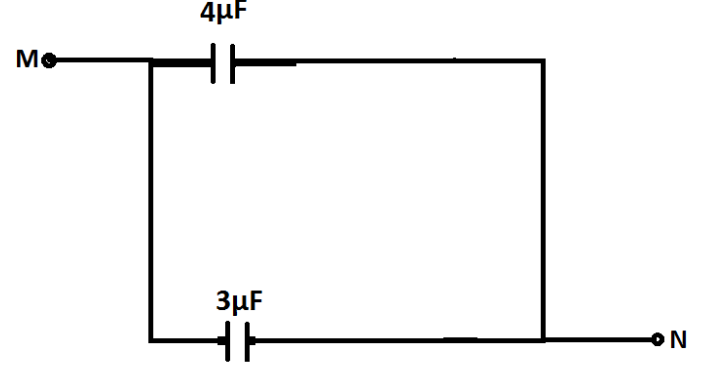
Finally, we can see that two capacitors of $4\mu F$and $3\mu F$ are connected in parallel connection. Therefore their equivalent capacitance can be determined by the formula ${C_{eq}} = {C_1} + {C_2}$ as $4 + 3 = 7\mu F$.
Thus the effective capacitance between points M and N is $7\mu F$.

Hence, option D is the right answer.

Note: The most important thing in this type of question to consider is to check for the short circuited capacitance. When the capacitor is short circuited, there is zero capacitance in a short circuited capacitor. It will behave as a conducting wire in the circuit.