Question

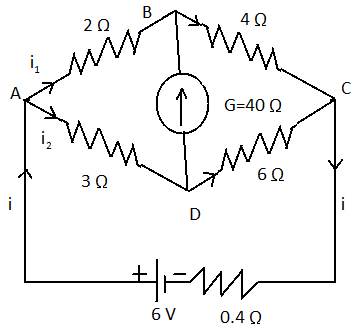
Calculate the currents $i, {i_1}$ and ${i_2}$ in given Wheatstone’s network of resistors, the internal resistance of the 6 V battery is $0.4\,\Omega$.

Answer 1

The concept of wheatstone bridge should be known before solving this problem. It is an arrangement where four resistances are connected in series so as to form a rectangle. Galvanometer is connected at the diagonal of the rectangle.
For balanced Wheatstone bridge the ratio of resistances of one side of the leg of Wheatstone bridge is equal to the ratio of resistances of the other leg of it.

Complete step by step solution:
Given: voltage supply by battery is 6 V.
The internal resistance of the battery is $0.4\,\Omega$.
Wheatstone resistances are $2\,\Omega ,4\,\Omega ,3\,\Omega \,{\rm{and}}\,6\,\Omega$.
First we determine the equivalent resistance of Wheatstone as shown below.
$R_{eq} = \dfrac{{6 \times 9}}{{6 + 9}}\\\ \Rightarrow 3.6 \Omega$
Total resistance of the circuit will be the sum of the equivalent resistance of Wheatstone and the internal resistance of the body. So the total resistance of network is calculated as,
$R = 3.6 + 0.4\\\ \Rightarrow 4\,\Omega$
The current flowing in circuit determined by the expression written as,
$i = \dfrac{V}{R}$
We can substitute the values in the above expression.
$i = \dfrac{6}{4}\\\ \Rightarrow 1.5 A$
Thus the value of i is 1.5 A.
This current $i$ is distributed in Wheatstone bridge. So the equation of current can be written as,
$i = {i_1} + {i_2}\\\ \Rightarrow 1.5 = {i_1} + {i_2}$ ................... (1)
The voltage difference between point A and C can be write as,
$6{i_1} - 9{i_2} = 0$ ………………(2)
From equation (1) and (2) we can determine the value of ${i_1}$ and ${i_2}$.
By solving the above equations we get ${i_1} = 0.9\,A$ and ${i_2} = 0.6 A$.

Note: Determine the equivalent resistance of Wheatstone bridge correctly because if you calculate the wrong resistance then it will give you an incorrect solution. Resistances are connected in series parallel combinations so determine according to their combination of resistances.