Question

Calculate the current shown by the ammeter in the circuit.

Answer 1

Learn how to calculate resistance of a parallel circuit. Redraw the diagram by using a simpler parallel and series circuit to find the equivalent resistance of the circuit and use Ohm’s law to find the current.

Formula used:
The ohm’s law is given by,
$V = IR$
where,$V$ is the voltage across the circuit component $I$ is the current through the circuit and $R$is the resistance of the element.
Equivalent resistance connected in series is given by,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ...$
The equivalent resistance in a parallel circuit is given by,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ....$
where, ${R_{eq}}$ is the equivalent resistance of the circuit and ${R_1}$ ,${R_2}$… are the resistances connected in parallel.

Complete step by step answer:
We have given here the circuit in the figure. We have to find the current through the ammeter, which is the same as the net current through the circuit. To find the net current we have to find the net resistance of the circuit. Now, the circuit can be redrawn as follows.

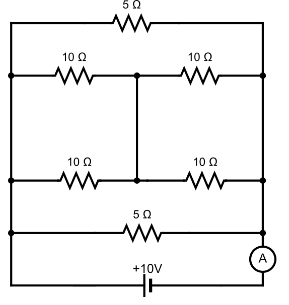
Now, in this circuit the connection of the four $10\Omega$ resistance are in parallel and the two parallel branches are in series connections

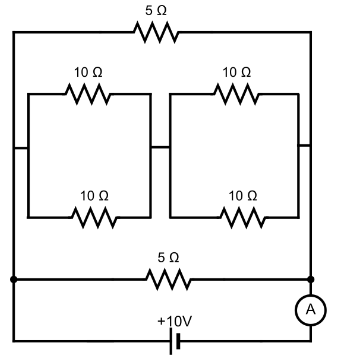
Hence, the resistance of the $10\Omega$branch will be,
$\dfrac{{10 \times 10}}{{10 + 10}} + \dfrac{{10 \times 10}}{{10 + 10}} = 2 \times 5 = 10\Omega$
Hence, we can redraw the circuit as:

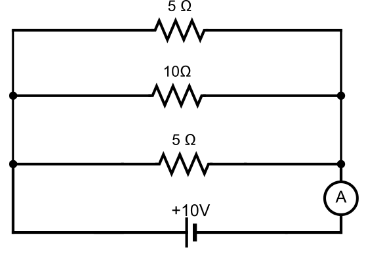
Hence, all the resistance are in parallel. So, the equivalent resistance of the circuit will be,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{10}} + \dfrac{1}{5} + \dfrac{1}{5}$
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{10}} + \dfrac{2}{5}$
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{1 + 4}}{{10}}$
$\therefore {R_{eq}} = \dfrac{{10}}{5} = 2$
Hence, equivalent resistance of the circuit is $2\Omega$.

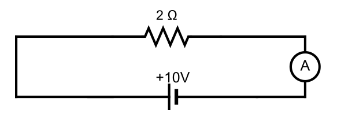
Hence, the current through the circuit will be $I = \dfrac{{10}}{2} = 5\,A$.

Note: To solve this type of question first realize the circuit and redraw it. Then, look for parallel and series combinations in the branches to find the equivalent resistance of the circuit. The series connection is only established when the resistance are joined end to end while for parallel connections they are joined at the same ends. Keep this always in mind while redrawing the circuit.