Question

Calculate the area enclosed by the circle of radius 0.56m to the correct number of significant figures.

Answer 1

Everything in this universe encloses some area. The area enclosed by a circle is determined by the product of $\pi$ and square of the radius and the solution demands for the significant figures so we will write the correct decimal value of $\pi$.

Complete step by step answer:
A circle is a 2D object having no thickness and only two dimensions with center O. Here we are given a circle of 0.56m radius.

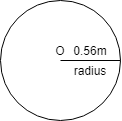
Area of the circle is given by the formula, $\pi \times {r^2}$
The value of $\pi$ is 3.14 and the radius is given as 0.56m
On substituting the value of both in the area of the circle, $3.14 \times 0.56 \times 0.56$
Which is equal to $0.9856{m^2}$. So, the area enclosed by a circle of radius 0.56m is $0.9856{m^2}$
If we write it in the significant figures then it will be equal to $0.99{m^2}$
Hence, the area enclosed by the circle of radius 0.56m in significant figures is 0.99${m^2}$

Additional information:
A circle is a 2D object as stated above but when we talk about a 3D object then a circle is known as a sphere and has a different formula for the area and volume
Area of sphere =$4\pi {r^2}$
And volume of sphere =$\dfrac{4}{3}\pi {r^3}$ where r is the radius
There are some important points regarding the circle which might be asked in a different question
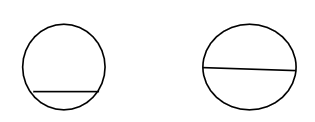
The sector of a circle: A circle can be divided into many parts as a sector as shown in fig.

Chord of a circle: A chord divides the circle into two parts. It may or may not divide into equal parts as shown in the diagram.

Note:
It is important to remember answering the question in the correct unit. This is the thing where most students make mistakes. Suppose the radius is in meters then the area will also be in the meter until it is asked in the question to change the unit.
In some questions, we might be given the diameter of the circle or asking us not to change the value of $\pi$. In that case, it is important to remember that 2r=D, where $r$ is the radius and $D$, is the diameter.
The significant figures are the number of digits in a value, often a measurement, that contributes to the degree of accuracy of the value. We start counting significant figures at the first non-zero digit.