Solveeit Logo
Login

Question

Question: Calculate tensions \({T_1}\), \( {T_2} \) and \( {T_3} \) in the given system when whole system is m...

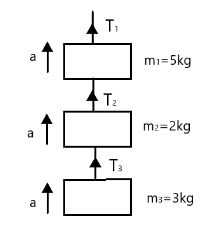
Calculate tensions T1{T_1}, T2{T_2} and T3{T_3} in the given system when whole system is moving upward with an acceleration of a=2m/s2a = 2m/{s^2}

Explanation

Solution

The tension in a particular string is affected by the weight of the boxes below it, whether immediate or not. Since the boxes accelerate upward, the force in the upward direction acting on a particular box is greater than the force acting in the downward direction. So in the equation of motion of each body we need to substitute the values and then we will get the answer.

Formula used: In this solution we will be using the following formulae;
W=mgW = mg where WW is the weight of a body, mm is the mass of the body and gg is the acceleration due to gravity.
F⃗NET=ma⃗{\vec F_{NET}} = m\vec a where FNET{F_{NET}} is the net force acting on a body, and a is the acceleration of the body.

Complete step by step solution:
In the diagram, the weight of all boxes acts on string T1{T_1} , while the weight of mass m2{m_2} and mass m3{m_3} acts on string T2{T_2} , but only the weight of mass m3{m_3} acts on string is T3{T_3} .
To find the tension in each string we analyse the dynamics of each box. For simplicity, let’s start from the bottom
For the bottom box, the tension T3{T_3} acts as the upward force acting on the box to pull it upward (as if to prevent it from falling), while the weight of the box acts downward. Hence, on the bottom box, Newton's second law would be given as
FNET=T3−W3=m3a{F_{NET}} = {T_3} - {W_3} = {m_3}a (assuming upward is positive), aa is positive (and non-zero) because the whole system accelerates upward, hence, the tension pulling the box must be greater than the weight.
Now, since the weight of a body is given as W=mgW = mg then
⇒T3−m3g=m3a\Rightarrow {T_3} - {m_3}g = {m_3}a
Making T3{T_3} subject, we have
⇒T3=m3a+m3g=m3(a+g)\Rightarrow {T_3} = {m_3}a + {m_3}g = {m_3}(a + g)
Inserting all known values
⇒T3=3(2+9.8)=35.4N\Rightarrow {T_3} = 3\left( {2 + 9.8} \right) = 35.4N
For the box of mass m2{m_2} , there are three forces acting on it.
The tension T2{T_2} acting upward, the weight W2{W_2} acting downwards, and finally the tension T3{T_3} acting downwards.
Therefore, we have
⇒FNET=T2−T3−W2=m2a\Rightarrow {F_{NET}} = {T_2} - {T_3} - {W_2} = {m_2}a
⇒T2=m2(a+g)+T3\Rightarrow {T_2} = {m_2}(a + g) + {T_3}
Inserting values, we have
⇒T2=2(2+9.8)+35.4=59N\Rightarrow {T_2} = 2\left( {2 + 9.8} \right) + 35.4 = 59N
Similarly for top box we have
⇒FNET=T1−T2−W1=m1a\Rightarrow {F_{NET}} = {T_1} - {T_2} - {W_1} = {m_1}a
⇒T1=m1(a+g)+T2\Rightarrow {T_1} = {m_1}(a + g) + {T_2}
Inserting values, we have
⇒T1=5(2+9.8)+59\Rightarrow {T_1} = 5(2 + 9.8) + 59
⇒T1=82.6N\Rightarrow {T_1} = 82.6N
Hence, T1=82.6N{T_1} = 82.6N , T2=59N{T_2} = 59N , and T3=35.4N{T_3} = 35.4N .

Note:
To avoid confusion, the tension T3{T_3} acts downward on the middle box because the action of the tension T3{T_3} acting on the bottom box has an equal and opposite tension acting downwards on the middle box. This is analogous to a box suspended by a string attached to a roof. The tension in this string acting upwards keeps the box suspended but at the same time, the string pulls on the roof downwards as though to bring it down.