Question

Calculate: $\sin \left( {2\arcsin \dfrac{3}{5}} \right)$

Answer 1

To proceed with the solution first we will find out the sin value by using pythagoras theorem later we will use the properties of Inverse Trigonometric Functions to find the value of the given expression.

Complete step-by-step solution:
According to the question. We have to find the value of $\sin \left( {2\arcsin \frac{3}{5}} \right)$
Now, to find the value of $\sin \left( {2\arcsin \dfrac{3}{5}} \right)$
Let us assume that $\arcsin \dfrac{3}{5} = \theta \\\ \\\$
Then, $\dfrac{3}{5} = \sin \theta$
Or, $\sin \theta = \dfrac{3}{5}....................(i)$
Now let us consider a right angled$\Delta ABC$, right angled at B.

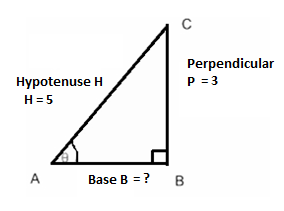
So, we know $\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}....................(ii)$
So, comparing (i) and (ii) we get:
$\dfrac{3}{5} = \dfrac{{perpendicular}}{{hypotenuse}}$
That is, Perpendicular = 3 and Hypotenuse = 5.
Using Pythagoras Theorem:
${\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {perpendicular} \right)^2} \\\ \Rightarrow {\left( 5 \right)^2} = {\left( {base} \right)^2} + {\left( 3 \right)^2} \\\ \Rightarrow 25 - 9 = {\left( {base} \right)^2} \\\ \Rightarrow {\left( {base} \right)^2} = 16 \\\ \Rightarrow \left( {base} \right) = \sqrt {16} \\\ \Rightarrow base = \pm 4 \\\$
Now, to find the value of $\sin \left( {2\arcsin \dfrac{3}{5}} \right)$
Putting $\arcsin \dfrac{3}{5} = \theta$in $\sin \left( {2\arcsin \dfrac{3}{5}} \right)$
It will now become as $\sin \left( {2\theta } \right)$
Now using the trigonometric formula for expanding $\sin \left( {2\theta } \right)$:
$\sin \left( {2\theta } \right) = 2\sin \theta \cos \theta$
So, using the values of the Right angled$\Delta ABC$,
We will get $\cos \theta = \dfrac{{base}}{{hypotenuse}}$
So base=4 and hypotenuse = 5, putting these values we get
$\cos \theta = \dfrac{4}{5}$,
So with $\sin \theta = \dfrac{3}{5}$ and $\cos \theta = \dfrac{4}{5}$, the expression will now become:
$\sin \left( {2\theta } \right) = 2\sin \theta \cos \theta \\\ = 2 \times \dfrac{3}{5} \times \dfrac{4}{5} \\\ = \dfrac{{24}}{{25}} \\\$

Hence, the value of $\sin \left( {2\arcsin \dfrac{3}{5}} \right)$ is $\dfrac{{24}}{{25}}$.

Note: While using the expansion for a trigonometric multiple angle like$\sin \left( {2\theta } \right)$, careful observation has to be made, if the trigonometric function taken is incorrect then the expansion will change and so will the corresponding solution. The expansion of trigonometric ratio is to be used depending on the trigonometric ratio mentioned in the term outside the arc trigonometric ratio. For example, instead of sin in $\sin \left( {2\arcsin \dfrac{3}{5}} \right)$, if we have cos that is, $\cos \left( {2\arcsin \dfrac{3}{5}} \right)$, then we will use the expansion of $\cos \left( {2\theta } \right)$,which is given as ${\cos ^2}\theta - {\sin ^2}\theta$ or $2{\cos ^2}\theta - 1$ or$1 - 2{\sin ^2}\theta$ .