Question
Question: Calculate \( \sin (2\arctan 2) \)...
Calculate sin(2arctan2)
Solution
Hint : Here the question is related to the trigonometry where it contains the sine and tan function. The question is exactly related to inverse trigonometry because we see “arctan” which means tan inverse. Hence by applying the inverse trigonometry we can find the result.
Complete step-by-step answer :
The question is given as sin(2arctan2)
Now let us consider the x=arctan2 --- (1)
We know that the inverse is also called an arc. Therefore the equation (1) can be written as
x=tan−1(2) --------- (2)
The equation (2) can be written as
tanx=2 ---------- (3)
By the considering the triangle we can define the tanx
Let us consider the right angled triangle ABC
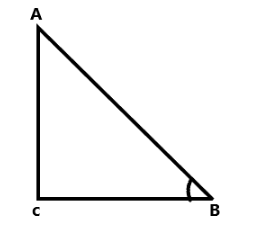
tanx=adjacentopposite=BCAC
⇒12=BCAC
Therefore the value of AC=2 and BC=1
By applying the Pythagoras theorem we have
AB2=AC2+BC2 ⇒AB2=(2)2+(1)2 ⇒AB2=4+1 ⇒AB2=5 ⇒AB=5
Hence the length of the AB= 5
Now we have to find the value of sin2x
We know the trigonometry formula that is sin2x=2.sinx.cosx ----(4)
By considering the triangle we can find the value of sine and cosine.
So we have
sinx=hypothesisopposite=ABAC
As we know the value. Substituting we have
⇒sinx=52 ---- (5)
cosx=hypothesisadjacent=ABBC
As we know the value. Substituting we have
⇒cosx=51 ---- (6)
Substituting the equation (5) and equation (6) in equation (4) we have
sin2x=2sinx.cosx ⇒sin2x=2×52×51 ⇒sin2x=54
Hence we have obtained the required result.
Therefore, the value of sin(2arctan2)=54
So, the correct answer is “ 54 ”.
Note : The inverse is also called an arc. This word is used in question very rare. In most questions they will ask directly like find the inverse. The sine function, cosine function and tan function are defined by considering the right angled triangle. Hence we know about the Pythagoras theorem and to which type of triangle it is applicable.
