Question

Calculate moment of Inertia of ring and sphere.

Answer 1

We will assume its mass and radius and then we will use the perpendicular axis theorem to find the moment of inertia of the ring. For the sphere we will cut a small piece of it where its thickness would be small then integrating the whole part we will find the moment of inertia of the sphere.

Complete step by step answer:
Moment of Inertia of ring: Let the mass of the ring be $M$ and radius $R$.

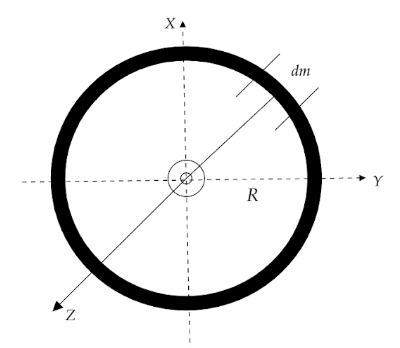
The moment of inertia of a ring about an axis passing through its center and perpendicular to its plane is given by,
${I_z} = \int {{R^2}} dm$
${I_z}= {R^2}\int_0^M {dm} \\\ \Rightarrow {I_z}= M{R^2} \\\$
The moment of inertia of the ring when the axis pass through its diameter is,
From perpendicular axis theorem,
${I_Z} = {I_x} + {I_y}$
When the axis passes through its diameter then ${I_x} = {I_y}$.
Thus, $${I_x} = {I_y}$$$ = \dfrac{{M{R^2}}}{2}$. The moment of inertia of a ring about an axis passing through its center and perpendicular to its plane is$M{R^2}$and when the axis pass through its diameter is$\dfrac{{M{R^2}}}{2}$.

Moment of Inertia of Sphere: Let the mass of the sphere be $M$ and radius $R$.

We can divide a sphere into concentric hollow spheres. Consider a hollow sphere of radius of $r$ and thickness $dr$. Let moment of inertia of hollow sphere is $dl$ then moment of inertia of solid sphere is the sum of moments of inertia of hollow spheres. Moment of inertia of an element considered as shown in figure.
$dl = \dfrac{2}{3}\left( {mass} \right) \times {r^2}$ $- - - \left( 1 \right)$
But mass=density$\times$volume$= \rho \times 4\pi {r^2}dr$

Putting the value of mass in equation $\left( 1 \right)$
$dl = \dfrac{8}{3}\pi \rho {r^4}dr$
Integrating the equation we get,
$I = \int\limits_0^R {dl = \dfrac{{8\pi \rho }}{3}} \int\limits_0^R {{r^4}} dr \Rightarrow I= \dfrac{{8\pi \rho }}{3} \times \dfrac{{{R^5}}}{5}$
Now putting $\rho = \dfrac{M}{{4\pi {R^3}}}$ we get,
$I = \dfrac{{8\pi }}{3} \times \dfrac{M}{{\dfrac{{4\pi {R^3}}}{3}}} \times \dfrac{{{R^5}}}{5} \therefore I= \dfrac{2}{5}M{R^2}$
So, the moment of inertia of the sphere is $\dfrac{2}{5}M{R^2}$.

Note: We must use the perpendicular axis theorem for the ring as it gives different values in different axes but for the sphere it is the same everywhere. We should consider small parts of the ring adjoined together for a sphere. Use of mass, density and volume altogether is mandatory.