Question
Question: Calculate equivalent capacitance between A and B in the circuit as shown. (A). \(6\mu F\) (B). \...
Calculate equivalent capacitance between A and B in the circuit as shown.
(A). 6μF
(B). 1.5μF
(C). zero
(D). 2μF
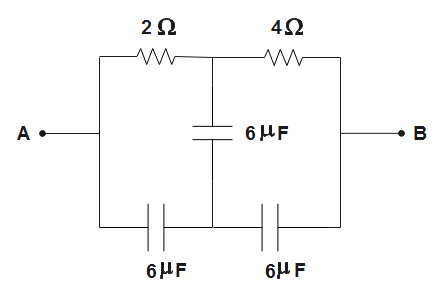
Solution
The circuit contains capacitors as well as resistors. The potential drop on each component will be different. Using Kirchhoff’s laws, we can calculate the potential on each component. Also check if it is a Wheatstone bridge circuit to simplify it. Furthermore, check if the resulting combination is series or parallel to find equivalent capacitance.
Formula used:
C1=C11+C21
Complete step-by-step solution:
Given, a circuit contains capacitors as well as resistors between two points A and B.
Kirchhoff's current law states that the total sum of charge at a junction or node of a circuit is zero. This means that the total incoming charge is equal to the total outgoing charge.
Kirchhoff's voltage law states that in a closed loop, the total potential is equal to the potential drop on each component connected in the loop.
The potential drop on a capacitor is-
V=CQ - (1)
Here,
Q is the charge stored on capacitor
C is the capacitance of the capacitor
The potential drop on the resistor is-
V′=IR
I is the current in the circuit
R is the resistance
Using Kirchhoff’s laws to solve the above circuit, we get,
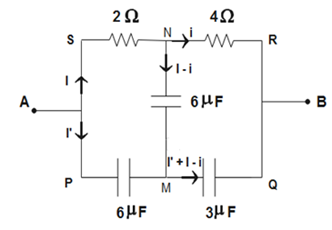
As we can see from the figure, the resistors and capacitors are in the same ratio.
∴42=36=21
Therefore, according to the Wheatstone bridge, no current will flow through the middle branch so the capacitor in the middle branch short-circuits. The new circuit will be-
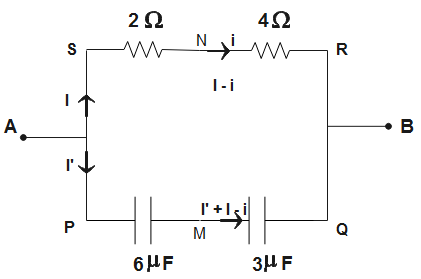
The capacitors are in series, so their equivalent will be-
C1=C11+C21⇒C1=61+31⇒C1=21
∴C=2μF
The equivalent capacitance of the circuit is 2μF. So, the correct option is (D).
Note:
According to the Wheatstone bridge, if components in the branches of a parallelogram are in the same ratio, then no current passes through the middle branch as the potential difference at the end points of the middle branch is the same. Capacitors can either be connected in series or parallel and their combinations are analogous to resistors.
