Solveeit Logo
Login

Question

Question: Calculate charge on 2µ F capacitor:- ...

Calculate charge on 2µ F capacitor:-

A

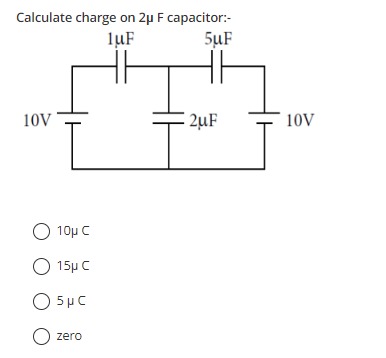
10µ C

B

15µ C

C

5µ C

D

zero

Answer

15µ C

Explanation

Solution

The circuit diagram shows two 10V batteries connected in parallel, with their positive terminals connected to a common point and their negative terminals connected to another common point. Let's label the nodes. Let the bottom wire be at potential VD=0VV_D = 0V. Then the top wire connected to the positive terminals of the batteries is at potential VA=10VV_A = 10V. Let the potential at the junction between the bottom plates of the 1 µF and 5 µF capacitors and the top plate of the 2 µF capacitor be VBV_B.

The 1 µF capacitor is connected between nodes A and B. The voltage across it is VAB=VA−VB=10−VBV_{AB} = V_A - V_B = 10 - V_B. The charge on it is Q1=C1VAB=1(10−VB)Q_1 = C_1 V_{AB} = 1(10 - V_B). The 5 µF capacitor is connected between nodes A and B. The voltage across it is VAB=VA−VB=10−VBV_{AB} = V_A - V_B = 10 - V_B. The charge on it is Q5=C5VAB=5(10−VB)Q_5 = C_5 V_{AB} = 5(10 - V_B). The 2 µF capacitor is connected between nodes B and D. The voltage across it is VBD=VB−VD=VB−0=VBV_{BD} = V_B - V_D = V_B - 0 = V_B. The charge on it is Q2=C2VBD=2VBQ_2 = C_2 V_{BD} = 2V_B.

In a steady state, the net charge on an isolated conductor or set of connected conductors remains constant. Consider the junction at node B. The plates connected to node B are the bottom plate of the 1 µF capacitor, the bottom plate of the 5 µF capacitor, and the top plate of the 2 µF capacitor. Assuming the capacitors were initially uncharged, the total charge on this isolated system of plates is zero.

The charge on the bottom plate of the 1 µF capacitor is −Q1=−(10−VB)=VB−10-Q_1 = -(10 - V_B) = V_B - 10. The charge on the bottom plate of the 5 µF capacitor is −Q5=−5(10−VB)=5VB−50-Q_5 = -5(10 - V_B) = 5V_B - 50. The charge on the top plate of the 2 µF capacitor is Q2=2VBQ_2 = 2V_B.

By conservation of charge, the sum of charges on these plates is zero: (VB−10)+(5VB−50)+2VB=0(V_B - 10) + (5V_B - 50) + 2V_B = 0 8VB−60=08V_B - 60 = 0 8VB=608V_B = 60 VB=608=152=7.5VV_B = \frac{60}{8} = \frac{15}{2} = 7.5 V

The voltage across the 2 µF capacitor is V2μF=VB=7.5VV_{2\mu F} = V_B = 7.5V. The charge on the 2 µF capacitor is Q2=C2V2μF=2µF×7.5V=15µCQ_2 = C_2 V_{2\mu F} = 2 µF \times 7.5 V = 15 µC.

The final answer is 15µ C.

Explanation of the solution:

  1. Assign potentials to the nodes. Set the potential of the bottom wire to 0V and the top wire to 10V due to the batteries. Let the potential of the intermediate junction be VBV_B.

  2. Write the voltage across each capacitor in terms of the node potentials.

  3. Write the charge on each capacitor using Q=CVQ=CV.

  4. Apply the principle of charge conservation to the isolated junction at potential VBV_B. The sum of charges on the plates connected to this junction is zero.

  5. Solve the resulting equation for VBV_B.

  6. Calculate the charge on the 2 µF capacitor using its capacitance and the voltage across it.